
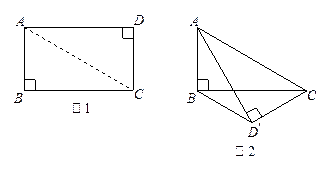 如图1,矩形纸片ABCD中,AB=4,BC=4
如图1,矩形纸片ABCD中,AB=4,BC=4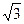 ,将矩形纸片沿对角线AC向下翻折,点D落在点D’处,联结B D’,如图2,求线段BD’ 的长.
,将矩形纸片沿对角线AC向下翻折,点D落在点D’处,联结B D’,如图2,求线段BD’ 的长.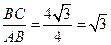 ,
,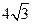 ,∠1=∠DAC=30°,
,∠1=∠DAC=30°,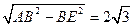 ,∴D’E=AD’—AE=
,∴D’E=AD’—AE=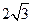 ,
,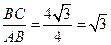 ,
,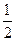 ∠BOA=30°,…………………………………………………………4分
∠BOA=30°,…………………………………………………………4分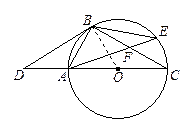 ∵∠4=∠BAC—∠1=30°,∴∠2=∠4,∴BD’=AB=4.
∵∠4=∠BAC—∠1=30°,∴∠2=∠4,∴BD’=AB=4. 

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:不详 题型:单选题
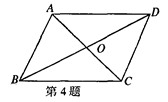
| A.OA=OC,OB=OD | B.∠BAD=∠BCD,AB∥CD |
| C.AD∥BC,AD=BC | D.AB=CD,AO=CO |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
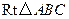 中,
中,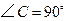 ,
,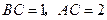 ,把边长分别为
,把边长分别为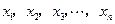 的
的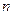 个正方形依次放入
个正方形依次放入 中,请回答下列问题:
中,请回答下列问题: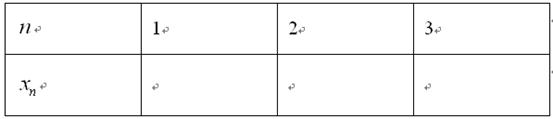
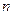 个正方形的边长
个正方形的边长 ;
;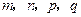 是正整数,且
是正整数,且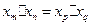 ,试判断
,试判断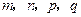 的关系.
的关系.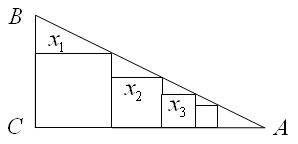
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
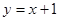 与y轴交于点
与y轴交于点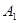 ,以
,以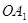 为边作正方形
为边作正方形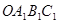 然后延长
然后延长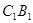 与直线
与直线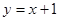 交于点
交于点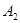 ,得到第一个梯形
,得到第一个梯形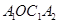 ;再以
;再以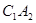 为边作正方形
为边作正方形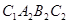 ,同样延长
,同样延长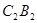 与直线
与直线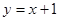 交于点
交于点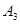 得到第二个梯形
得到第二个梯形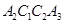 ;,再以
;,再以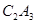 为边作正方形
为边作正方形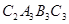 ,延长
,延长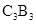 ,得到第三个梯形;……则第2个
,得到第三个梯形;……则第2个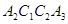
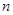 (n是正整数)个梯形的面积是 (用含n的式子
(n是正整数)个梯形的面积是 (用含n的式子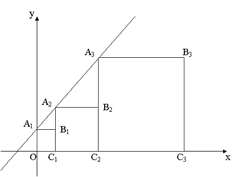
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 泸州,21,5分)如图,已知D是△ABC的边AB上一点,CE∥AB,DE交
泸州,21,5分)如图,已知D是△ABC的边AB上一点,CE∥AB,DE交 AC于点O,且OA=OC,猜想线段CD与线段AE的大小关系和位置关系,并加以证明.
AC于点O,且OA=OC,猜想线段CD与线段AE的大小关系和位置关系,并加以证明.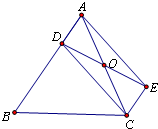
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com