
【题目】如图,CD⊥AB,EF⊥AB,垂足分别为D、F,∠1=∠2,若∠A=65°,∠B=45°,求∠AGD的度数.

【答案】70°
【解析】
由CD⊥AB,EF⊥AB可得出∠CDF=∠EFB=90°,利用“同位角相等,两直线平行”可得出CD∥EF,利用“两直线平行,同位角相等”可得出∠DCB=∠1,结合∠1=∠2可得出∠DCB=∠2,利用“内错角相等,两直线平行”可得出DG∥BC,利用“两直线平行,同位角相等”可得出∠ADG的度数,在△ADG中,利用三角形内角和定理即可求出∠AGD的度数.
解:∵CD⊥AB,EF⊥AB,
∴∠CDF=∠EFB=90°,
∴CD∥EF,
∴∠DCB=∠1.
∵∠1=∠2,
∴∠DCB=∠2,
∴DG∥BC,
∴∠ADG=∠B=45°.
又∵在△ADG中,∠A=65°,∠ADG=45°,
∴∠AGD=180°﹣∠A﹣∠ADG=70°


 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:
【题目】如图,将直角三角形ABC沿着BC方向平移![]() cm得到直角三角形DEF,AB=5cm,BC=8cm,DH=2cm,那么图中阴影部分的面积为____ cm 2.
cm得到直角三角形DEF,AB=5cm,BC=8cm,DH=2cm,那么图中阴影部分的面积为____ cm 2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD为等边△ABC的高,E、F分别为线段AD、AC上的动点,且AE=CF,当BF+CE取得最小值时,∠AFB=( )
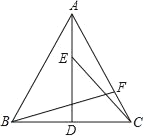
A. 112.5°B. 105°C. 90°D. 82.5°
查看答案和解析>>
科目:初中数学 来源: 题型:
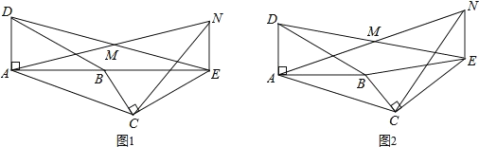
【题目】如图,已知△BAD≌△BCE,∠BAD=∠BCE=90°,∠ABD=∠BEC=30°,点 M 为 DE的中点,过点E与AD平行的直线交射线AM于点 N.
(1)如 图 1,当 A、B、E三点在同一直线上时,
①求证:△MEN≌△MDA;
②判断 AC与 CN数量关系为_______,并说明理由.
(2)将图 1 中△BCE绕 点 B 逆时针旋转一周,旋转过程中△CAN 能否为等腰直角三角形?若能,直接写出旋转角度;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个正整数能表示成两个连续偶数的平方差,那么这个正整数为“神秘数”.
如:![]()
![]()
![]()
因此,4,12,20这三个数都是神秘数.
(1)28和2012这两个数是不是神秘数?为什么?
(2)设两个连续偶数为![]() 和
和![]() (其中
(其中![]() 为非负整数),由这两个连续偶数构造的神秘数是4的倍数,请说明理由.
为非负整数),由这两个连续偶数构造的神秘数是4的倍数,请说明理由.
(3)两个连续奇数的平方差(取正数)是不是神秘数?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点D、E分别是∠B的两边BC、BA上的点,∠DEB=2∠B,F为BA上一点.
(1)如图①,若DF平分∠BDE,求证:BD=DE+EF;
(2)如图②,若DF为△DBE的外角平分线,BD、DE、EF三者有怎样的数量关系?请证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2008年8月第29届奥运会将在北京开幕,5个城市的国际标准时间(单位:时)在数轴上表示如图所示,那么北京时间2008年8月8日20时应是( )
![]()
A. 伦敦时间2008年8月8日11时
B. 巴黎时间2008年8月8日13时
C. 纽约时间2008年8月8日5时
D. 汉城时间2008年8月8日19时
查看答案和解析>>
科目:初中数学 来源: 题型:
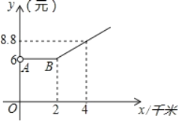
【题目】某市的出租车收费y(元)与路程x(千米)之间的函数关系如图所示.
(1)图中AB段的意义是 .
(2)当x>2时,y与x的函数关系式为 .
(3)张先生打算乘出租车从甲地去丙地,但需途径乙地办点事,已知甲地到乙地的路程为1km,乙地至丙地的路程超过3km,现有两种打车方案:
方案一:先打车从甲地到乙地,办完事后,再打另一部出租车去丙地;
方案二:先打车从甲地到乙地,让出租车司机等候,办完事后,继续乘该车去丙地(出租车等候期间,张先生每分钟另付0.2元,假设计价器不变).
张先生应选择哪种方案较为合算?试说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com