
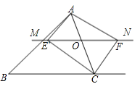
【题目】如图,在△ABC中,AB=AC,∠A=36°,BD,CE是角平分线,则图中的等腰三角形共有

A. 8个 B. 7个 C. 6个 D. 5个
【答案】A
【解析】
根据三角形内角和定理求出∠ABC=∠ACB=72°,根据角平分线求出∠ABD=∠DBC=∠ACE=∠ECB=36°,根据三角形内角和定理求出∠BDC、∠BEC、∠EOB、∠DOC,根据等腰三角形的判定推出即可.
∵AB=AC,∠A=36°,
∴∠ABC=∠ACB=![]() (180°∠A)=72°,
(180°∠A)=72°,
∵BD,CE是角平分线,
∴∠ABD=∠DBC=![]() ∠ABC=36°,∠ACE=∠ECB=36°,
∠ABC=36°,∠ACE=∠ECB=36°,
∴∠A=∠ABD=∠ACE,∠DBC=∠ECB,
∴∠BDC=180°∠ACB∠DBC=180°72°36°=72°,
同理∠BEC=72°,
∴∠BDC=∠ACB,∠BEC=∠EBC,
∴∠EOB=180°∠BEC∠EBD=180°72°36°=72°,
同理∠DOC=72°,
∴∠BEO=∠BOE,∠CDO=∠COD,
即等腰三角形有△OBC,△ADB,△AEC,△BEC,△BDC,△ABC,△EBO,△DCO,共8个,
故选:A.


科目:初中数学 来源: 题型:
【题目】如图,利用关于坐标轴对称的点的坐标特点
(1) 作出△ABC关于x轴对称的图象.
(2) 写出A、B、C的对应点A′、B′、C′的坐标.
(3) 直接写出△ABC的面积__________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)6a(a﹣2)﹣(2﹣3a)2;
(2)(2x2﹣3y)(2x2+3y)﹣2x(﹣3x3);
(3)先化简,再求值:[2(x﹣y)]2﹣(12x3y2﹣18x2y3)÷(3xy2),其中x=﹣3,y=﹣![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,点
中,点![]() 是
是![]() 边上的一个动点,过点
边上的一个动点,过点![]() 作直线
作直线![]() ,设
,设![]() 交
交![]() 的平
的平
分线于点![]() ,交
,交![]() 的外角平分线于点
的外角平分线于点![]() .
.
![]() 求证:
求证:![]() ;
;
![]() 当点
当点![]() 运动到何处时,四边形
运动到何处时,四边形![]() 是矩形?为什么?
是矩形?为什么?
![]() 进行怎样的变化才能使
进行怎样的变化才能使![]() 边上存在点
边上存在点![]() ,使四边形
,使四边形![]() 是正方形?为什么?
是正方形?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】CD是线段AB的垂直平分线,则∠CAD=∠CBD.请说明理由.

解:∵CD是线段AB的垂直平分线(已知),
∴AC=______,______=BD(______)
在△ADC和______中,
______=BC,
AD=______,
CD=______(______),
∴______≌______(______ ).
∴∠CAD=∠CBD (全等三角形的对应角相等).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】动漫节开幕前,某动漫公司预测某种动漫玩具能够畅销,就分两批分别用32000元和68000元购进了这种玩具销售,其中第二批购进数量是第一批购进数量的2倍,但每套进价多了10元.
(1)该动漫公司这两批各购进多少套玩具?
(2)如果这两批玩具每套售价相同,且全部销售后总利润不少于20000元,那么每套售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,点O是等边三角形ABC内一点,∠AOB=110°,∠BOC=α, 以OC为边作等边三角形OCD,连接AD.

(1)当α=150°时,试判断△AOD的形状,并说明理由;
(2)探究:当a为多少度时,△AOD是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形![]() 中,∠D=100°,∠DAB的平分线AE交DC于点E,连接BE,若AE=AB,则∠EBC的度数为( )
中,∠D=100°,∠DAB的平分线AE交DC于点E,连接BE,若AE=AB,则∠EBC的度数为( )
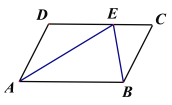
A.30°B.50°C.80°D.100°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com