
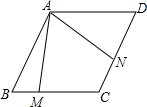
 如图,在?ABCD中,∠ABC=60°,AB=BC=6cm,点M、N分别在BC和CD上,且∠MAN=60°,则四边形AMCN的面积是多少( )
如图,在?ABCD中,∠ABC=60°,AB=BC=6cm,点M、N分别在BC和CD上,且∠MAN=60°,则四边形AMCN的面积是多少( )| A. | 6cm2 | B. | 18cm2 | C. | 9$\sqrt{3}$cm2 | D. | 8$\sqrt{3}$cm2 |
分析 连接AC,通过证明△ABM和△ANC全等可知四边形AMCN的面积正好等于平行四边形面积的一半.
解答 解:连接AC,
∵∠B=60°,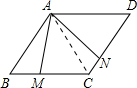
∴∠BAD=120°,
∵∠MAN=60°,
∴∠BAM=∠CAN,
∴△ABC为等边三角形,
∴AB=AC,
∴△ABM≌△ACN,
∴四边形AMCN的面积等于平行四边形面积的一半.
∵AB=6cm,
∴BC边上的高为3$\sqrt{3}$,S菱形ABCD=6×$3\sqrt{3}$=18$\sqrt{3}$,
∴四边形AMCN的面积等于$\frac{1}{2}$×18$\sqrt{3}$=9$\sqrt{3}$.
故选C.
点评 本题考查了等边三角形的判定和性质、平行四边形的性质、平行四边形的面积公式以及勾股定理的运用,题目比较简单.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | y1>y2 | B. | y1<y2 | C. | y1=y2 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 一组对边平行且相等,一个角是直角 | |
| B. | 对角线互相平分且相等 | |
| C. | 有三个角是直角 | |
| D. | 一组对边平行,另一组对边相等,且对角线相等 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,数轴上表示的是某个函数自变量的取值范围,则这个函数解析式( )
如图,数轴上表示的是某个函数自变量的取值范围,则这个函数解析式( )| A. | y=2x-5 | B. | y=2x2+7 | C. | y=$\frac{1}{x(x+1)}$ | D. | y=$\sqrt{x+2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏.如图,是一局象棋残局,已知表示棋子“馬”和“車”的点的坐标分别为(4,3),(-2,1),则表示棋子“炮”的点的坐标为( )
象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏.如图,是一局象棋残局,已知表示棋子“馬”和“車”的点的坐标分别为(4,3),(-2,1),则表示棋子“炮”的点的坐标为( )| A. | (1,3) | B. | (3,2) | C. | (0,3) | D. | (-3,3) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com