【题目】已知直线l1：y=﹣ 与直线l2：y=kx﹣ 交于x轴上的同一个点A，直线l1与y轴交于点B，直线l2与y轴的交点为C．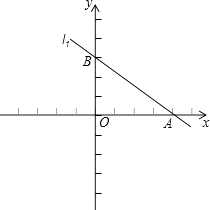

（1）求k的值，并作出直线l2图象；
（2）若点P是线段AB上的点且△ACP的面积为15，求点P的坐标；
（3）若点M、N分别是x轴上、线段AC上的动点（点M不与点O重合），是否存在点M、N，使得△ANM≌△AOC？若存在，请求出N点的坐标；若不存在，请说明理由．

参考答案：

【答案】
（1）解：∵直线l1：y=﹣ x+3与x轴交于点A，

∴令y=0时，x=4，即A（4，0），

将A（4，0）代入直线l2：y=kx﹣ ，得k= ，

直线l2图象如图1所示；


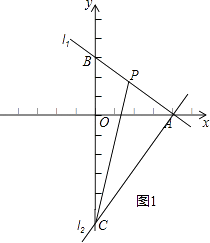
（2）解：设P（a，b），

根据题意得：S△ACP=S△ABC﹣S△PBC= ×（3+ ）×4﹣ ×（3+ ）a=15，

解得：a= ，

将P（ ，b）代入直线l1得：b= ×（﹣ ）+3=﹣ +3= ，

∴点P的坐标（ ， ）


（3）解：如图2，作ND⊥x轴于D，

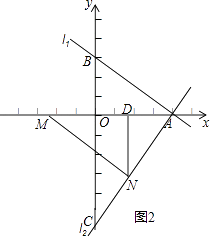
∵AC= = ，△ANM≌△AOC，

∴AM=AC= ，AN=AO=4，MN=OC= ，∠ANM=∠AOC=90°，

∵S△AMN= AMND= ANMN，

∴ND= = = ，

将N的纵坐标y=﹣ 代入直线l2得：x= ，

∴当N的纵坐标为（ ，﹣ ）时，△ANM≌△AOC


【解析】（1）对于直线l1，令y=0求出x的值，确定出A坐标，代入直线l2求出k的值，作出直线l2图象即可；
（2）设P（a，b），由S△ACP=S△ABC-S△BPC，求出a的值，进而求出b的值，确定出P坐标即可；
（3）如图2，作ND⊥x轴于D，利用勾股定理求出AC的长，由△ANM≌△AOC，得到对应边相等，表示出AM，AN，MN，确定出△AMN为直角三角形，利用面积法求出ND的长，确定出N纵坐标，进而求出横坐标，确定出N坐标即可．

【考点精析】本题主要考查了确定一次函数的表达式和全等三角形的性质的相关知识点，需要掌握确定一个一次函数，需要确定一次函数定义式y=kx+b（k不等于0）中的常数k和b．解这类问题的一般方法是待定系数法；全等三角形的对应边相等; 全等三角形的对应角相等才能正确解答此题．

关闭