Question

【题目】如图，排球运动员站在点O处练习发球，将球从O点正上方2m的A处发出，把球看成点，其运行的高度y（m）与运行的水平距离x（m）满足关系式y=a（x﹣6）2+h．已知球网与O点的水平距离为9m，高度为2.43m，球场的边界距O点的水平距离为18m．

（1）当h=2.6时，求y与x的关系式（不要求写出自变量x的取值范围）

（2）当h=2.6时，球能否越过球网？球会不会出界？请说明理由；

（3）若球一定能越过球网，又不出边界，求h的取值范围．

Answer 1

【答案】y=﹣（x﹣6）2+2.6，h≥

【解析】

试题分析：（1）利用h=2.6将点（0，2），代入解析式求出即可；

（2）利用当x=9时，y=﹣（x﹣6）2+2.6=2.45，当y=0时，，分别得出即可；

（3）根据当球正好过点（18，0）时，抛物线y=a（x﹣6）2+h还过点（0，2），以及当球刚能过网，此时函数解析式过（9，2.43），抛物线y=a（x﹣6）2+h还过点（0，2）时分别得出h的取值范围，即可得出答案．

试题解析：解：（1）∵h=2.6，球从O点正上方2m的A处发出，

∴抛物线y=a（x﹣6）2+h过点（0，2），

∴2=a（0﹣6）2+2.6，

解得：a=﹣，

故y与x的关系式为：y=﹣（x﹣6）2+2.6，

（2）当x=9时，y=﹣（x﹣6）2+2.6=2.45＞2.43，

所以球能过球网；

当y=0时，，

解得：x1=6+2＞18，x2=6﹣2（舍去）

故会出界；

（3）当球正好过点（18，0）时，抛物线y=a（x﹣6）2+h还过点（0，2），代入解析式得：

，

解得：，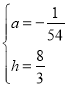

此时二次函数解析式为：y=﹣（x﹣6）2+，

此时球若不出边界h≥，

当球刚能过网，此时函数解析式过（9，2.43），抛物线y=a（x﹣6）2+h还过点（0，2），代入解析式得：

，

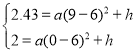解得：，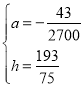

此时球要过网h≥，

故若球一定能越过球网，又不出边界，h的取值范围是：h≥．