
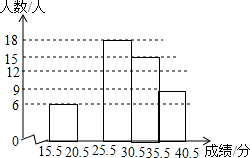
 某学校为了了解八年级400名学生期末考试的体育测试成绩,从中随机抽取了部分学生的成绩(满分40分,而且成绩均为整数),绘制了频数分布表与频数分布直方图(如图).
某学校为了了解八年级400名学生期末考试的体育测试成绩,从中随机抽取了部分学生的成绩(满分40分,而且成绩均为整数),绘制了频数分布表与频数分布直方图(如图).| 分组 | 频数 | 频率 |
| 15.5~20.5 | 6 | 0.10 |
| 20.5~25.5 | a | 0.20 |
| 25.5~30.5 | 18 | 0.30 |
| 30.5~35.5 | 15 | b |
| 35.5~40.5 | 9 | 0.15 |
分析 (1)根据第一组的频数是6,对应的频率是0.10,则调查的总人数即可求解;
(2)根据(1)即可直接求解;
(3)根据(1)即可求解;
(4)利用总人数乘以对应的频率即可求解.
解答 解:(1)调查的总人数是:6÷0.10=60(人),
则a=60×0.20=12(人),
b=$\frac{15}{60}$=0.25;
故答案是:12,0.25;
(2)如图2所示 ;
;
(3)样本容量是:60;
(4)∵所抽查的学生中3(0分)以上(不含30分)的人数有15+9=24(人)
∴估计全校达到优良水平的人数约为:400×$\frac{24}{60}$=160(人).
点评 本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
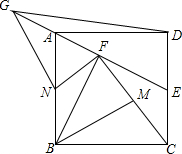 正方形ABCD中,E为CD中点,BF⊥AE于F,M为CF上一点,将△BMF绕点F顺时针旋转得△GNF,M的对应点N点恰好在AB边上,B的对应点G恰好在线段EA的延长线上.若CM=$\frac{\sqrt{5}}{2}$,则DG的长为$\sqrt{10}$.
正方形ABCD中,E为CD中点,BF⊥AE于F,M为CF上一点,将△BMF绕点F顺时针旋转得△GNF,M的对应点N点恰好在AB边上,B的对应点G恰好在线段EA的延长线上.若CM=$\frac{\sqrt{5}}{2}$,则DG的长为$\sqrt{10}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com