
(12分)如图,抛物线与x轴相交于B,C两点,与y轴相交于点A,点P(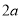 ,
,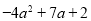 )(a是任意实数)在抛物线上,直线
)(a是任意实数)在抛物线上,直线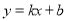 经过A,B两点.
经过A,B两点.
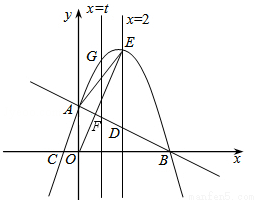
(1)求直线AB的解析式;
(2)平行于y轴的直线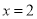 交直线AB于点D,交抛物线于点E.
交直线AB于点D,交抛物线于点E.
①直线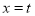 (0≤t≤4)与直线AB相交F,与抛物线相交于点G.若FG∶DE=3∶4,求t的值;
(0≤t≤4)与直线AB相交F,与抛物线相交于点G.若FG∶DE=3∶4,求t的值;
②将抛物线向上平移m(m>0)个单位,当EO平分∠AED时,求m的值.
(1)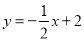 ;(2)①1或3;②
;(2)①1或3;②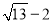 .
.
【解析】
试题分析:(1)根据点P的坐标,可得出抛物线解析式,然后求出A、B、C的坐标,利用待定系数法求出直线AB的解析式;
(2)①根据点E(2,5),D(2,1),G(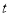 ,
,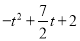 ),F(
),F(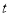 ,
,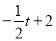 ),表示出DE、FG,再由FG:DE=3:4,可得出t的值;
),表示出DE、FG,再由FG:DE=3:4,可得出t的值;
②设点A(0,2+m),则点E(2,5+m),作AH⊥DE,垂足为H,在Rt△AEH中利用勾股定理求出AE,根据EO平分∠AED及平行线的性质可推出∠AEO=∠AOE,AO=AE,继而可得出m的值.
试题解析:(1)∵P(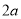 ,
,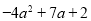 )(a是实数)在抛物线上,
)(a是实数)在抛物线上,
∴抛物线的解析式为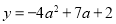 =
=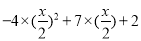 ﹣
﹣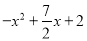 ,当
,当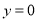 时,即
时,即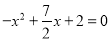 ,解得
,解得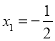 ,
,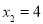 ,当x=0时,y=2.∴A(0,2),B(4,0),C(
,当x=0时,y=2.∴A(0,2),B(4,0),C(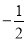 ,0),将点A、B的坐标代入
,0),将点A、B的坐标代入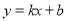 ,得:∴
,得:∴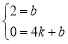 ,解得:
,解得: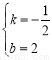 ,故直线AB的解析式为
,故直线AB的解析式为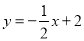 ;
;
(2)①∵点E(2,5),D(2,1),G(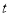 ,
,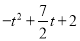 ),F(
),F(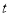 ,
,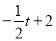 ),∴DE=4,FG=
),∴DE=4,FG=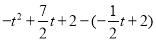 =
=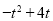 ,∵FG:DE=3:4,∴
,∵FG:DE=3:4,∴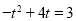 ,解得
,解得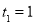 ,
,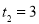 .
.
②设点A(0,2+m),则点E(2,5+m),作AH⊥DE,垂足为H,
∴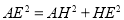 =
=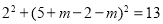 ,即AE=
,即AE=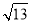 ,∵EO平分∠AED,∴∠AEO=∠DEO,∵AO∥ED,∴∠DEO=∠AOE,∴∠AEO=∠AOE,∴AO=AE,即
,∵EO平分∠AED,∴∠AEO=∠DEO,∵AO∥ED,∴∠DEO=∠AOE,∴∠AEO=∠AOE,∴AO=AE,即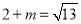 ,解得m=
,解得m=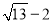 .
.

考点:二次函数综合题.


 培优三好生系列答案
培优三好生系列答案科目:初中数学 来源: 题型:解答题
(10分)如图,⊙ 的半径为4,
的半径为4, 是⊙
是⊙ 外一点,连接
外一点,连接 ,且
,且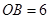 ,延长
,延长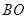 交⊙
交⊙ 于点
于点 ,点
,点 为⊙
为⊙ 上一点,过点
上一点,过点 作直线
作直线 的垂线,垂足为
的垂线,垂足为 ,
, 平分
平分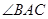 .
.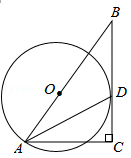
(1)求证: 是⊙
是⊙ 的切线;
的切线;
(2)求 的长.
的长.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省九年级上学期期中调研考试数学试卷(解析版) 题型:选择题
如图,⊙O的直径CD=10cm,弦AB⊥CD于M,OM∶OC=3∶5,则AB=( )
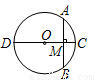
A.8cm B.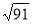 cm C.6cm D.2cm
cm C.6cm D.2cm
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省九年级上学期期中考试数学试卷(解析版) 题型:解答题
(10分)如图,在△ABC中,∠ABC=90°,D是边AC上的一点,连接BD,使∠A=2∠1,E是BC上的一点,以BE为直径的⊙O经过点D.

(1)求证:AC是⊙O的切线;
(2)若∠A=60°,⊙O的半径为2,求阴影部分的面积.(结果保留根号和π)
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省九年级上学期期中考试数学试卷(解析版) 题型:填空题
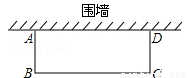
如图,邻边不等的矩形花圃ABCD,它的一边AD利用已有的围墙(可利用的围墙长度超过6 m),另外三边所围的栅栏的总长度是6 m.若矩形的面积为4 m2,则AB的长度是 ___________m.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年黑龙江省伊春市九年级11月月考数学试卷(解析版) 题型:解答题
(10分)某农户计划利用现有的一面墙(现在的墙足够长),建造如图所示的长方体水池,培育不同品种的鱼苗,他已备足可以修高为1.5 m,长18m的墙的材料准备施工,设图中与现有一面墙垂直的三面墙的长度都为xm,即AD=EF=BC=xm(不考虑墙的厚度).

(1)若想水池的总容积为36 m3 ,x应等于多少?
(2)若想使水池的总容积V最大,x应为多少?最大容积是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com