
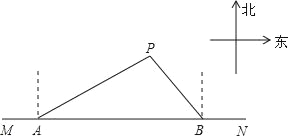
ЁОЬтФПЁПШчЭМЃЌдкЖЋЮїЗНЯђЕФКЃАЖЯпMNЩЯгаAЁЂBСНЫвДЌЃЌОљЪеЕНвбДЅНИИщЧГЕФДЌPЕФЧѓОШаХКХЃЌвбжЊДЌPдкДЌAЕФББЦЋЖЋ58ЁуЗНЯђЃЌДЌPдкДЌBЕФББЦЋЮї35ЁуЗНЯђЃЌAPЕФОрРыЮЊ30КЃРяЃЈВЮПМЪ§ОнЃКsin32ЁуЁж0.53ЃЌsin55ЁуЁж0.82ЃЉЃЎ
ЃЈ1ЃЉЧѓДЌPЕНКЃАЖЯпMNЕФОрРыЃЈОЋШЗЕН0.1КЃРяЃЉЃЛ
ЃЈ2ЃЉШєДЌAЁЂДЌBЗжБ№вд20КЃРя/аЁЪБЁЂ15КЃРя/аЁЪБЕФЫйЖШЭЌЪБГіЗЂЃЌдШЫйжБЯпЧАЭљОШдЎЃЌЪдЭЈЙ§МЦЫуХаЖЯФФЫвДЌЯШЕНДяДЌPДІЃЎ
ЁОД№АИЁПЃЈ1ЃЉДЌPЕНКЃАЖЯпMNЕФОрРыдМЮЊ15.9КЃРяЃЛЃЈ2ЃЉBДЌЯШЕНДяЃЎ
ЁОНтЮіЁПНтЃКЃЈ1ЃЉШчЭМЃЌЙ§ЕуPзїPHЁЭMNгкЕуH,
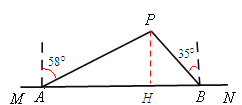
ЁпДЌPдкДЌAЕФББЦЋЖЋ58ЁуЗНЯђЃЌЁрЁЯPAH=320ЁЃ
ЁпAP=30КЃРяЃЌ
Ёр![]() ЃЈКЃРяЃЉЁЃ
ЃЈКЃРяЃЉЁЃ
Д№ЃКДЌPЕНКЃАЖЯпMNЕФОрРыЮЊ15.9КЃРяЁЃ
ЃЈ2ЃЉЁпДЌPдкДЌBЕФББЦЋЮї35ЁуЗНЯђЃЌЁрЁЯPBH=550ЁЃ
Ёр![]() ЃЈКЃРяЃЉЁЃ
ЃЈКЃРяЃЉЁЃ
ЁпДЌAЁЂДЌBЕФЫйЖШЗжБ№ЮЊ20КЃРя/аЁЪБЁЂ15КЃРя/аЁЪБЃЌ
ЁрДЌAЕНДяДЌPЕФЪБМфЮЊ![]() ЃЈаЁЪБЃЉЃЌДЌBЕНДяДЌPЕФЪБМфЮЊ
ЃЈаЁЪБЃЉЃЌДЌBЕНДяДЌPЕФЪБМфЮЊ![]() ЃЈаЁЪБЃЉЁЃ
ЃЈаЁЪБЃЉЁЃ
Ёп![]() ЃЌЁрДЌBЯШЕНДяДЌPЁЃ
ЃЌЁрДЌBЯШЕНДяДЌPЁЃ
ЃЈ1ЃЉЙ§ЕуPзїPHЁЭMNгкЕуH,ЙЙдьжБНЧШ§НЧаЮPAHЃЌгІгУе§ЯвКЏЪ§МДПЩЧѓЕУДЌPЕНКЃАЖЯпMNЕФОрРыPHЁЃ
ЃЈ2ЗжБ№ЧѓГіСНДЌAЕНДяДЌPЕФЪБМфНјааБШНЯМДПЩЕУГіНсТлЁЃ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєЙигкxЕФвЛдЊЖўДЮЗНГЬx2Љ2ЃЈ2ЉkЃЉx+k2+12=0гаЪЕЪ§ИљІСЁЂІТЃЎ
ЃЈ1ЃЉЧѓЪЕЪ§kЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉЩш![]() ЃЌЧѓtЕФзюаЁжЕЃЎ
ЃЌЧѓtЕФзюаЁжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЭМжаЭјИёЩЯАДвЊЧѓЛГіЭМаЮЃЌВЂЛиД№ЮЪЬтЃК
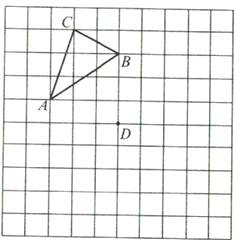
ЃЈ1ЃЉШчЙћНЋШ§НЧаЮ![]() ЦНвЦЃЌЪЙЕУЕу
ЦНвЦЃЌЪЙЕУЕу![]() ЦНвЦЕНЭМжаЕу
ЦНвЦЕНЭМжаЕу![]() ЮЛжУЃЌЕу
ЮЛжУЃЌЕу![]() ЁЂЕу
ЁЂЕу![]() ЕФЖдгІЕуЗжБ№ЮЊЕу
ЕФЖдгІЕуЗжБ№ЮЊЕу![]() ЁЂЕу
ЁЂЕу![]() ЃЌЧыЛГіШ§НЧаЮ
ЃЌЧыЛГіШ§НЧаЮ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЛГіШ§НЧаЮ![]() ЙигкЕу
ЙигкЕу![]() ГЩжааФЖдГЦЕФШ§НЧаЮ
ГЩжааФЖдГЦЕФШ§НЧаЮ![]() ЃЎ
ЃЎ
ЃЈ3ЃЉШ§НЧаЮ![]() гыШ§НЧаЮ
гыШ§НЧаЮ![]() ______ЃЈЬюЁАЪЧЁБЛђЁАЗёЁБЃЉЙигкФГИіЕуГЩжааФЖдГЦЃПШчЙћЪЧЃЌЧыдкЭМжаЛГіетИіЖдГЦжааФЃЌВЂМЧзїЕу
______ЃЈЬюЁАЪЧЁБЛђЁАЗёЁБЃЉЙигкФГИіЕуГЩжааФЖдГЦЃПШчЙћЪЧЃЌЧыдкЭМжаЛГіетИіЖдГЦжааФЃЌВЂМЧзїЕу![]() ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃЕФДКМОШЄЮЖдЫЖЏЛсЩюЪмбЇЩњЯВАЎЃЌИУаЃЬхг§НЬЪІЮЊСЫСЫНтИУДЮдЫЖЏЛсжаЫФИіЯюФПЕФЪмЛЖгГЬЖШЃЌЫцЛњГщШЁСЫВПЗжбЇЩњНјааЮЪОэЕїВщЃЌБЛЕїВщбЇЩњаыДгЁАЭаЧђХмЁЂжРЗЩХЬЁЂЭЦаЁГЕЁЂбМзгВНЁБЫФИіЯюФПжабЁдёздМКзюЯВЛЖЕФвЛЯюЃЎ
ИљОнЕїВщНсЙћЃЌЬхг§НЬЪІЛцжЦСЫЭМ1КЭЭМ2СНИіЭГМЦЭМЃЈОљЮДЭъГЩЃЉЃЌЧыИљОнЭМ1КЭЭМ2ЕФаХЯЂЃЌНтД№ЯТСаЮЪЬтЃЎ
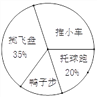
(1)ДЫДЮЙВЕїВщСЫЖрЩйУћбЇЩњЃП
(2)НЋЬѕаЮЭГМЦЭМВЙГфЭъећЃЎ
(3)ЭМ2жаЁАбМзгВНЁБЫљдкЩШаЮдВаФНЧЮЊЖрЩйЖШЃП
(4)ШєШЋаЃгабЇЩњ1600ШЫЃЌЙРМЦИУаЃЯВЛЖЁАЭЦаЁГЕЁБЯюФПЕФбЇЩњШЫЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНЋЭМЂйжаЕФе§ЗНаЮМєПЊЕУЕНЭМЂкЃЌЭМЂкжаЙВга4Иіе§ЗНаЮЃЛНЋЭМЂкжаЕФвЛИіе§ЗНаЮМєПЊЕУЕНЭМЂлЃЌЭМЂлжаЙВга7Иіе§ЗНаЮЃЛНЋЭМЂлжаЕФвЛИіе§ЗНаЮМєПЊЕУЕНЭМЂмЃЌЭМЂмжаЙВга10Иіе§ЗНаЮЁЁШчДЫЯТШЅЃЌдђЕк2019ИіЭМжаЙВгае§ЗНаЮЕФИіЪ§ЮЊЃЈ ЃЉЃЎ
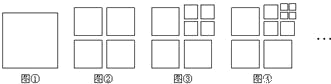
A.6052B.6055C.6058D.6061
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
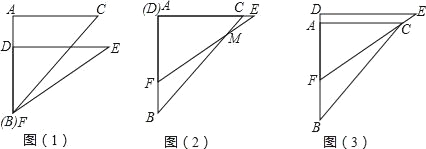
ЁОЬтФПЁПЁОЬтФПЁПгавЛИБжБНЧШ§НЧАхЃЌдкШ§НЧАхABCжаЃЌЁЯBAC=90ЁуЃЌAB=AC=6ЃЌдкШ§НЧАхDEFжаЃЌЁЯFDE=90ЁуЃЌDF=4ЃЌDE=![]() ЃЎНЋетИБжБНЧШ§НЧАхАДШчЭМ1ЫљЪОЮЛжУАкЗХЃЌЕуBгыЕуFжиКЯЃЌжБНЧБпBAгыFDдкЭЌвЛЬѕжБЯпЩЯЃЎЯжЙЬЖЈШ§НЧАхABCЃЌНЋШ§НЧАхDEFбиЩфЯпBAЗНЯђЦНаавЦЖЏЃЌЕБЕуFдЫЖЏЕНЕуAЪБЭЃжЙдЫЖЏЃЎ
ЃЎНЋетИБжБНЧШ§НЧАхАДШчЭМ1ЫљЪОЮЛжУАкЗХЃЌЕуBгыЕуFжиКЯЃЌжБНЧБпBAгыFDдкЭЌвЛЬѕжБЯпЩЯЃЎЯжЙЬЖЈШ§НЧАхABCЃЌНЋШ§НЧАхDEFбиЩфЯпBAЗНЯђЦНаавЦЖЏЃЌЕБЕуFдЫЖЏЕНЕуAЪБЭЃжЙдЫЖЏЃЎ
ЃЈ1ЃЉШчЭМ2ЃЌЕБШ§НЧАхDEFдЫЖЏЕНЕуDгыЕуAжиКЯЪБЃЌЩшEFгыBCНЛгкЕуMЃЌдђЁЯEMC=ЁЁ ЖШЃЛ
ЃЈ2ЃЉШчЭМ3ЃЌдкШ§НЧАхDEFдЫЖЏЙ§ГЬжаЃЌЕБEFОЙ§ЕуCЪБЃЌЧѓFCЕФГЄЃЛ
ЃЈ3ЃЉдкШ§НЧАхDEFдЫЖЏЙ§ГЬжаЃЌЩшBF=xЃЌСНПщШ§НЧАхжиЕўВПЗжЕФУцЛ§ЮЊyЃЌЧѓyгыxЕФКЏЪ§НтЮіЪНЃЌВЂЧѓГіЖдгІЕФxШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
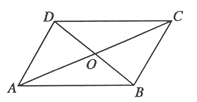
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮABCDжаЃЌACЃЌBDЯрНЛгкЕуOЃЌOЪЧACЕФжаЕуЃЌAD//BCЃЌAC=8,BD=6.
ЃЈ1ЃЉЧѓжЄЃКЫФБпаЮABCDЪЧЦНааЫФБпаЮЃЛ
ЃЈ2ЃЉШєACЁЭBDЃЌЧѓЁѕABCDЕФУцЛ§.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃга3000УћбЇЩњЃЎЮЊСЫНтШЋаЃбЇЩњЕФЩЯбЇЗНЪНЃЌИУаЃЪ§бЇаЫШЄаЁзщвдЮЪОэЕїВщЕФаЮЪНЃЌЫцЛњЕїВщСЫИУаЃВПЗжбЇЩњЕФжївЊЩЯбЇЗНЪН(ВЮгыЮЪОэЕїВщЕФбЇЩњжЛФмДгвдЯТСљИіжжРржабЁдёвЛРр)ЃЌВЂНЋЕїВщНсЙћЛцжЦГЩШчЯТВЛЭъећЕФЭГМЦЭМЃЎ
жжРр | A | B | C | D | E | F |
ЩЯбЇЗНЪН | ЕчЖЏГЕ | ЫНМвГЕ | ЙЋЙВНЛЭЈ | здааГЕ | ВНаа | ЦфЫћ |
ФГаЃВПЗжбЇЩњжївЊЩЯбЇЗНЪНЩШаЮЭГМЦЭМФГаЃВПЗжбЇЩњжївЊЩЯбЇЗНЪНЬѕаЮЭГМЦЭМ
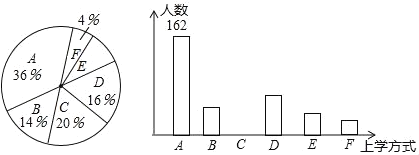
ИљОнвдЩЯаХЯЂЃЌЛиД№ЯТСаЮЪЬтЃК
(1)ВЮгыБОДЮЮЪОэЕїВщЕФбЇЩњЙВга____ШЫЃЌЦфжабЁдёBРрЕФШЫЪ§га____ШЫЃЎ
(2)дкЩШаЮЭГМЦЭМжаЃЌЧѓEРрЖдгІЕФЩШаЮдВаФНЧІСЕФЖШЪ§ЃЌВЂВЙШЋЬѕаЮЭГМЦЭМЃЎ
(3)ШєНЋAЁЂCЁЂDЁЂEетЫФРрЩЯбЇЗНЪНЪгЮЊЁАТЬЩЋГіааЁБЃЌЧыЙРМЦИУаЃУПЬьЁАТЬЩЋГіааЁБЕФбЇЩњШЫЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊMЪЧЁїABCЕФБпABЕФжаЕуЃЌDЪЧMCЕФбгГЄЯпЩЯвЛЕуЃЌТњзуЁЯACM=ЁЯBDMЃЎ
(1)ЧѓжЄЃКAC=BDЃЛ
(2)ШєЁЯBMC=60ЁуЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com