
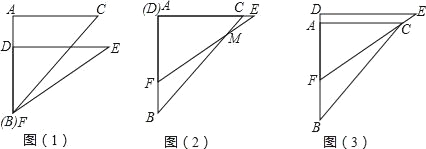
【题目】【题目】有一副直角三角板,在三角板ABC中,∠BAC=90°,AB=AC=6,在三角板DEF中,∠FDE=90°,DF=4,DE=![]() .将这副直角三角板按如图1所示位置摆放,点B与点F重合,直角边BA与FD在同一条直线上.现固定三角板ABC,将三角板DEF沿射线BA方向平行移动,当点F运动到点A时停止运动.
.将这副直角三角板按如图1所示位置摆放,点B与点F重合,直角边BA与FD在同一条直线上.现固定三角板ABC,将三角板DEF沿射线BA方向平行移动,当点F运动到点A时停止运动.
(1)如图2,当三角板DEF运动到点D与点A重合时,设EF与BC交于点M,则∠EMC= 度;
(2)如图3,在三角板DEF运动过程中,当EF经过点C时,求FC的长;
(3)在三角板DEF运动过程中,设BF=x,两块三角板重叠部分的面积为y,求y与x的函数解析式,并求出对应的x取值范围.
【答案】(1)15;(2)FC=![]() ;(3)y=
;(3)y=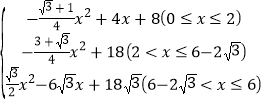 .
.
【解析】试题分析:(1)如题图2所示,由三角形的外角性质可得;
(2)如题图3所示,在Rt△ACF中,解直角三角形即可;
(3)认真分析三角板的运动过程,明确不同时段重叠图形的变化情况
(I)当0≤x≤2时,如图1所示;
(II)当2<x≤6-2![]() 时,如图2所示;
时,如图2所示;
(III)当6-2![]() <x≤6时,如图3所示.
<x≤6时,如图3所示.
试题解析:(1)如题图2所示,
∵在三角板DEF中,∠FDE=90°,DF=4,DE=4![]() ,
,
∴tan∠DFE=![]() =
=![]() ,∴∠DFE=60°,
,∴∠DFE=60°,
∴∠EMC=∠FMB=∠DFE-∠ABC=60°-45°=15°;
(2)如题图3所示,当EF经过点C时,
FC=![]() =
=![]() =
=![]() =4
=4![]() ;
;
(3)在三角板DEF运动过程中,
(I)当0≤x≤2时,如图1所示:
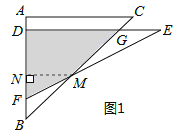
设DE交BC于点G.
过点M作MN⊥AB于点N,则△MNB为等腰直角三角形,MN=BN.
又∵NF=![]() =
=![]() MN,BN=NF+BF,
MN,BN=NF+BF,
∴NF+BF=MN,即![]() MN+x=MN,解得:MN=
MN+x=MN,解得:MN=![]() x.
x.
y=S△BDG-S△BFM
=![]() BDDG-
BDDG-![]() BFMN
BFMN
=![]() (x+4)2-
(x+4)2-![]() x
x![]() x
x
=-![]() x2+4x+8;
x2+4x+8;
(II)当2<x≤6-2![]() 时,如图2所示:
时,如图2所示:
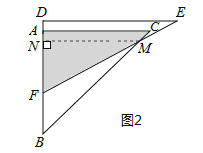
过点M作MN⊥AB于点N,则△MNB为等腰直角三角形,MN=BN.
又∵NF=![]() =
=![]() MN,BN=NF+BF,
MN,BN=NF+BF,
∴NF+BF=MN,即![]() MN+x=MN,解得:MN=
MN+x=MN,解得:MN=![]() x.
x.
y=S△ABC-S△BFM
=![]() ABAC-
ABAC-![]() BFMN
BFMN
=![]() ×62-
×62-![]() x
x![]() x
x
=-![]() x2+18;
x2+18;
(III)当6-2![]() <x≤6时,如图3所示:
<x≤6时,如图3所示:
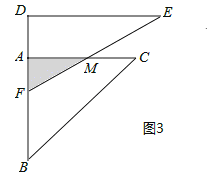
由BF=x,则AF=AB-BF=6-x,
设AC与EF交于点M,则AM=AFtan60°=![]() (6-x).
(6-x).
y=S△AFM=![]() AFAM=
AFAM=![]() (6-x)
(6-x)![]() (6-x)=
(6-x)=![]() x2-6
x2-6![]() x+18
x+18![]() .
.
综上所述,y与x的函数解析式为:
y=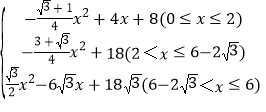 .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在方格纸中,点A,B,P都在格点上.请按要求画出以AB为边的格点四边形,使P在四边形内部(不包括边界上),且P到四边形的两个顶点的距离相等.

(1)在图甲中画出一个ABCD.
(2)在图乙中画出一个四边形ABCD,使∠D=90°,且∠A≠90°.(注:图甲、乙在答题纸上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为8,点E是BC上的一点,连接AE并延长交射线DC于点F,将△ABE沿直线AE翻折,点B落在点N处,AN的延长线交DC于点M,当AB=2CF时,则NM的长为_____.
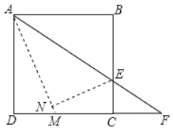
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,∠C=90°,∠A=30°,D为AC边上一点,且CD=2AD=4,过点D作DE⊥AB于点E.
(1)求AB的长;
(2)如图2,将△ADE绕点A顺时针旋转60°,延长DE交AC于点G,交AB于点F,连接CF.
求证:点F是AB的中点.
(3)如图3,在△ADE绕点A顺时针旋转的过程中,当DE的延长线恰好经过点B时,若点P为BD的中点,连接CP、PF.
求证:∠PCE=∠PEC.
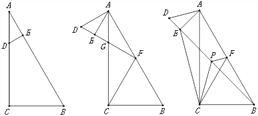
查看答案和解析>>
科目:初中数学 来源: 题型:
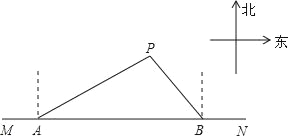
【题目】如图,在东西方向的海岸线MN上有A、B两艘船,均收到已触礁搁浅的船P的求救信号,已知船P在船A的北偏东58°方向,船P在船B的北偏西35°方向,AP的距离为30海里(参考数据:sin32°≈0.53,sin55°≈0.82).
(1)求船P到海岸线MN的距离(精确到0.1海里);
(2)若船A、船B分别以20海里/小时、15海里/小时的速度同时出发,匀速直线前往救援,试通过计算判断哪艘船先到达船P处.
查看答案和解析>>
科目:初中数学 来源: 题型:
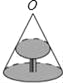
【题目】如图是圆桌正上方的灯泡O发出的光线照射桌面后,在地面上形成阴影(圆形)的示意图.已知桌面的直径为1.2m,桌面距离地面1m,若灯泡O距离地面3m,则地面上阴影部分的面积为_____m2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车专卖店销售A,B两种型号的新能源汽车.上周售出1辆A型车和3辆B型车,销售额为96万元;本周已售出2辆A型车和1辆B型车,销售额为62万元.
(1)求每辆A型车和B型车的售价各为多少万元?
(2)甲公司拟向该店购买A,B两种型号的新能源汽车共6辆,且A型号车不少于2辆,购车费不少于130万元,则有哪几种购车方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校的一个数学兴趣小组在本校学生中开展主题为“环广西公路自行车世界巡回赛”的专题调查活动,取随机抽样的方式进行问卷调查,问卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,分别记作A、B、C、D;并根据调查结果绘制成如图所示不完整的统计图,请结合图中信息解答下列问题:

(1)请求出本次被调查的学生共多少人,并将条形统计图补充完整.
(2)估计该校1500名学生中“C等级”的学生有多少人?
(3)在“B等级”的学生中,初三学生共有4人,其中1男3女,在这4个人中,随机选出2人进行采访,则所选两位同学中有男同学的概率是多少?请用列表法或树状图的方法求解.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com