
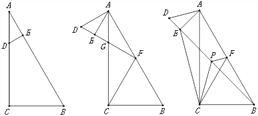
【题目】如图1,在△ABC中,∠C=90°,∠A=30°,D为AC边上一点,且CD=2AD=4,过点D作DE⊥AB于点E.
(1)求AB的长;
(2)如图2,将△ADE绕点A顺时针旋转60°,延长DE交AC于点G,交AB于点F,连接CF.
求证:点F是AB的中点.
(3)如图3,在△ADE绕点A顺时针旋转的过程中,当DE的延长线恰好经过点B时,若点P为BD的中点,连接CP、PF.
求证:∠PCE=∠PEC.
【答案】(1)4![]() ;(2)见解析;(3)见解析;
;(2)见解析;(3)见解析;
【解析】分析:(1)求出AC的长后,根据直角三角形中的30°角结合勾股定理求解;(2)判断△ADF是含30°角的直角三角形,则AD=2,由勾股定理求AF的长,结合AB的长求证;(3)证点B,C,P,F四点共圆得∠BPC=60°,证点A,E,C,B四点共圆得∠BEC=30°.
详解:(1)∵CD=2AD=4,∴AC=6,
设BC=x,则AB=2x.
在Rt△ABC中,由勾股定理得AB2=AC2+BC2,即(2x)2=62+x2.
解得,AB=![]() .
.
(2)由题意得:∠DAG=∠EAF=60°,∠D=90°-∠DAE=60°,
则∠DAB=90°,
所以DF=2AD=4,由勾股定理得AF=![]() ,
,
∴AF=![]() AB,即F是AB的中点.
AB,即F是AB的中点.
(3)∵点P,点F分别是BD,BA的中点,
∴PF∥AD,∴∠FPB=∠D=60°,
由(2)可知,AF=CF,
∵∠FCA=∠FAC=30°,∴∠BCF=60°,
∴∠FPB=∠BCF,∴C,B,F,P四点共圆,
∴∠CPB=∠CFB=60°,∵∠AEB=∠ACB=90°,
∴A,E,C,B四点共圆,∴∠CEP=∠CAB=30°,
∴∠ECP=∠CPB-∠CEP=30°,
∴∠PCE=∠PEC.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
【题目】现今“微信运动”被越来越多的人关注和喜爱,某兴趣小组随机调查了我市50名教师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表(不完整):
步数 | 频数 | 频率 |
0≤x<4000 | 8 | a |
4000≤x<8000 | 15 | 0.3 |
8000≤x<12000 | 12 | b |
12000≤x<16000 | c | 0.2 |
16000≤x<20000 | 3 | 0.06 |
20000≤x<24000 | d | 0.04 |
请根据以上信息,解答下列问题:
(1)写出a,b,c,d的值并补全频数分布直方图;
(2)本市约有37800名教师,用调查的样本数据估计日行走步数超过12000步(包含12000步)的教师有多少名?
(3)若在50名被调查的教师中,选取日行走步数超过16000步(包含16000步的两名教师与大家分享心得,求被选取的两名教师恰好都在20000步(包含20000步)以上的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上有三个点A,B,C,回答下列问题:
(1)若将点B向右移动6个单位后,三个点所表示的数中最小的数是多少?
(2)在数轴上找一点D,使点D到A,C两点的距离相等,写出点D表示的数;
(3)在点B左侧找一点E,使点E到点A的距离是到点B的距离的2倍,并写出点E表示的数.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
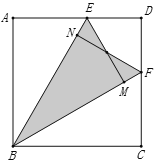
【题目】如图,正方形ABCD的边长为![]() ,点E、F分别为边AD、CD上一点,将正方形分别沿BE、BF折叠,点A的对应点M恰好落在BF上,点C的对应点N恰好落在BE上,则图中阴影部分的面积为_________.
,点E、F分别为边AD、CD上一点,将正方形分别沿BE、BF折叠,点A的对应点M恰好落在BF上,点C的对应点N恰好落在BE上,则图中阴影部分的面积为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校的春季趣味运动会深受学生喜爱,该校体育教师为了了解该次运动会中四个项目的受欢迎程度,随机抽取了部分学生进行问卷调查,被调查学生须从“托球跑、掷飞盘、推小车、鸭子步”四个项目中选择自己最喜欢的一项.
根据调查结果,体育教师绘制了图1和图2两个统计图(均未完成),请根据图1和图2的信息,解答下列问题.
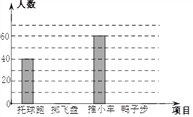
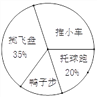
(1)此次共调查了多少名学生?
(2)将条形统计图补充完整.
(3)图2中“鸭子步”所在扇形圆心角为多少度?
(4)若全校有学生1600人,估计该校喜欢“推小车”项目的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场举行“促销周”活动,每个促销日顾客人数变化如下表(正号表示人数比前一天多,负号表示比前一天少)
日期 | 第1日 | 第2日 | 第3日 | 第4日 | 第5日 | 第6日 | 第7日 |
人数变化(单位:千人) |
|
|
|
|
|
|
|
(1)本“促销周”中顾客人数最多的一天比最少的一天多几千人?
(2)若第一个促销日前一天的顾客人数为3千人,则第3个促销日的顾客人数是多少千人?
(3)如果每千人每日带来的经济收入约为5万元,则该商场本“促销周”总收入约为多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
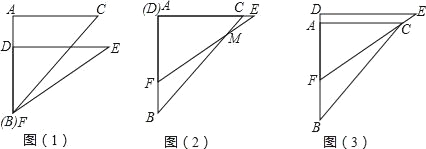
【题目】【题目】有一副直角三角板,在三角板ABC中,∠BAC=90°,AB=AC=6,在三角板DEF中,∠FDE=90°,DF=4,DE=![]() .将这副直角三角板按如图1所示位置摆放,点B与点F重合,直角边BA与FD在同一条直线上.现固定三角板ABC,将三角板DEF沿射线BA方向平行移动,当点F运动到点A时停止运动.
.将这副直角三角板按如图1所示位置摆放,点B与点F重合,直角边BA与FD在同一条直线上.现固定三角板ABC,将三角板DEF沿射线BA方向平行移动,当点F运动到点A时停止运动.
(1)如图2,当三角板DEF运动到点D与点A重合时,设EF与BC交于点M,则∠EMC= 度;
(2)如图3,在三角板DEF运动过程中,当EF经过点C时,求FC的长;
(3)在三角板DEF运动过程中,设BF=x,两块三角板重叠部分的面积为y,求y与x的函数解析式,并求出对应的x取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O为原点,A、B为数轴上两点,AB=15,且OA:OB=2:1,点P从点B以每秒4个单位的速度向右运动.
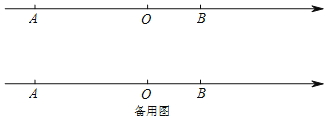
(1)A、B对应的数分别为 、 ;
(2)当点P运动时,分别取BP的中点E,AO的中点F,请画图,并求出![]() 的值;
的值;
(3)若当点P开始运动时,点A、B分别以每秒2个单位和每秒5个单位的速度同时向右运动,是否存在常数m,使得3AP+2OP﹣mBP为定值?若存在,请求出m的值以及这个定值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com