
����Ŀ����ͼ����OΪԭ�㣬A��BΪ���������㣬AB��15����OA��OB��2��1����P�ӵ�B��ÿ��4����λ���ٶ������˶���
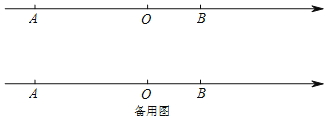
��1��A��B��Ӧ�����ֱ�Ϊ�� ������ ����
��2������P�˶�ʱ���ֱ�ȡBP���е�E��AO���е�F���뻭ͼ�������![]() ��ֵ��
��ֵ��
��3��������P��ʼ�˶�ʱ����A��B�ֱ���ÿ��2����λ��ÿ��5����λ���ٶ�ͬʱ�����˶����Ƿ���ڳ���m��ʹ��3AP+2OP��mBPΪ��ֵ�������ڣ������m��ֵ�Լ������ֵ���������ڣ���˵�����ɣ�
���𰸡���1����10��5����2����ͼ��������![]() ��2����3����m��14ʱ��Ϊ��ֵ55��
��2����3����m��14ʱ��Ϊ��ֵ55��
��������
��1������AB��15����OA��OB��2��1��ֱ�����OA��OB�ij��ȣ��Ӷ����A��B��Ӧ������
��2���������⻭ͼ���ɣ�Ȼ��![]() �ֱ���
�ֱ���![]() ��ʾ�������������ֵ.
��ʾ�������������ֵ.
��3���ֱ��ú�m�Ĵ���ʽ��ʾ��AP��OP��BP�������ж��Ƿ����mֵʹ3AP+2OP��mBPΪ��ֵ
��1����AB��15��OA��OB��2��1
��AO��10��BO��5
��A���Ӧ��Ϊ��10��B���Ӧ��Ϊ5��
�ʴ�Ϊ����10��5��
��2����ͼ���£�
![]()
����E��F�ֱ�ΪBP��AO���е�
��OF��![]() AO��BE��
AO��BE��![]() BP
BP
��EF��OF+OB+BE��![]() AO+OB+
AO+OB+![]() BP
BP
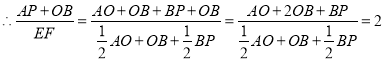
��3�����˶�ʱ��Ϊt�룬���P��Ӧ������5+4t����A��Ӧ��������10+2t����B��Ӧ������5+5t��
��AP��5+4t������10+2t����2t+15��OP��5+4t��BP��t��
��3AP+2OP��mBP��3��2t+15��+2��5+4t����mt����14��m��t+55��
����m��14ʱ��3AP+2OP��mBPΪ��ֵ55��


 ���ĺ����Ͼ�������ϵ�д�
���ĺ����Ͼ�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
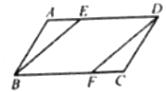
����Ŀ����ͼ����![]() ABCD�У���E��F�ֱ���AD��BC���ϣ���BE��DF.
ABCD�У���E��F�ֱ���AD��BC���ϣ���BE��DF.
��֤:(1)�ı���BFDE��ƽ���ı��Σ�
(2)AE=CF.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
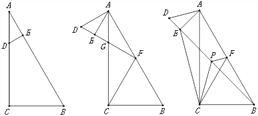
����Ŀ����ͼ1������ABC�У���C��90�㣬��A��30�㣬DΪAC����һ�㣬��CD��2AD��4������D��DE��AB�ڵ�E��
(1)��AB�ij���
(2)��ͼ2������ADE�Ƶ�A˳ʱ����ת60�����ӳ�DE��AC�ڵ�G����AB�ڵ�F������CF��
��֤����F��AB���е㣮
(3)��ͼ3������ADE�Ƶ�A˳ʱ����ת�Ĺ����У���DE���ӳ���ǡ�þ�����Bʱ������PΪBD���е㣬����CP��PF��
��֤����PCE����PEC��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
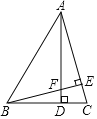
����Ŀ����ͼ����֪����ABC�У�BC���ϵĸ�AD��AC���ϵĸ�BE���ڵ�F���ҡ�BAC=45�㣬BD=6��CD=4������ABC�����Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
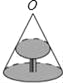
����Ŀ����ͼ��Բ�����Ϸ��ĵ���O�����Ĺ�������������ڵ������γ���Ӱ��Բ�Σ���ʾ��ͼ����֪�����ֱ��Ϊ1.2m������������1m��������O�������3m�����������Ӱ���ֵ����Ϊ_____m2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ�˽�ѧ���Ŀ����Ķ�������Բ���ѧ�������˵��飬��ͳ������ƽ��ÿ��Ŀ����Ķ�ʱ��t����λ��min����Ȼ�������������ݻ�������������������ͳ��ͼ��
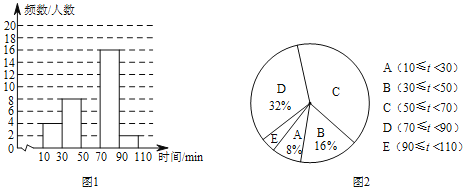
�������������Ϣ����������⣺
��1�����ε�����ȡ���� �����鷽ʽ�������������� ��
��2��ͼ2��C��Բ�ĽǶ���Ϊ�� �ȣ���ȫͼ1��Ƶ���ֲ�ֱ��ͼ��
��3����У��900��ѧ�������Ƹ�Уѧ��ƽ��ÿ��Ŀ����Ķ�ʱ�䲻����50min��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����ר��������A��B�����ͺŵ�����Դ����.�����۳�1��A�ͳ���3��B�ͳ������۶�Ϊ96��Ԫ���������۳�2��A�ͳ���1��B�ͳ������۶�Ϊ62��Ԫ.
��1����ÿ��A�ͳ���B�ͳ����ۼ۸�Ϊ������Ԫ��
��2����˾����õ깺��A��B�����ͺŵ�����Դ������6������A�ͺų�������2���������Ѳ�����130��Ԫ�������ļ��ֹ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
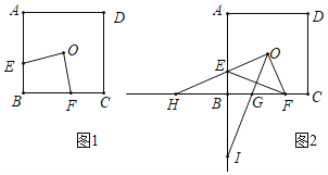
����Ŀ����ͼ1����![]() ��������
��������![]() �����ģ���
�����ģ���![]() ��
��![]() ����һ���㣬��
����һ���㣬��![]() �Ͻ�ȡ
�Ͻ�ȡ![]() ������
������![]() ��
��![]() ������̽�����ڵ�
������̽�����ڵ�![]() ���˶������У�
���˶������У�
(1)�����߶�![]() ��
��![]() �Ĺ�ϵ����˵�����ɣ�
�Ĺ�ϵ����˵�����ɣ�
����̽����
(2)��ͼ2������![]() ������
������![]() ��
��![]() �Ĵ��߽�
�Ĵ��߽�![]() �ڵ�
�ڵ�![]() ����
����![]() ���ӳ����ڵ�
���ӳ����ڵ�![]() ���ӳ�
���ӳ�![]() ��
��![]() ���ӳ����ڵ�
���ӳ����ڵ�![]() ��
��
��ֱ��д��![]() �Ķ�����
�Ķ�����
����![]() ����̽��
����̽��![]() ��ֵ�Ƿ�Ϊ��ֵ�����ǣ��������ֵ����֮����˵������
��ֵ�Ƿ�Ϊ��ֵ�����ǣ��������ֵ����֮����˵������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�ı���ABCD��ֱ��MN,��O��ֱ��MN��.
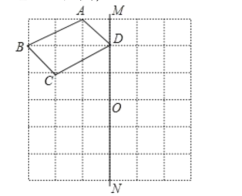
(1)�����ı���![]() ʹ�ı���
ʹ�ı���![]() ���ı���ABCD����ֱ��MN����Գƣ�
���ı���ABCD����ֱ��MN����Գƣ�
(2)�����ı���![]() ʹ�ı���
ʹ�ı���![]() ���ı���ABCD���ڵ�O�Գƣ�
���ı���ABCD���ڵ�O�Գƣ�
(3)�ı���![]() ���ı���
���ı���![]() ����Գƺ����ĶԳ������ǣ�����ͼ�ϻ����Գ����Գ�����.
����Գƺ����ĶԳ������ǣ�����ͼ�ϻ����Գ����Գ�����.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com