
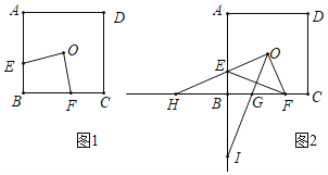
【题目】如图1,点![]() 是正方形
是正方形![]() 的中心,点
的中心,点![]() 是
是![]() 边上一动点,在
边上一动点,在![]() 上截取
上截取![]() ,连结
,连结![]() ,
,![]() .初步探究:在点
.初步探究:在点![]() 的运动过程中:
的运动过程中:
(1)猜想线段![]() 与
与![]() 的关系,并说明理由.
的关系,并说明理由.
深入探究:
(2)如图2,连结![]() ,过点
,过点![]() 作
作![]() 的垂线交
的垂线交![]() 于点
于点![]() .交
.交![]() 的延长线于点
的延长线于点![]() .延长
.延长![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
①直接写出![]() 的度数.
的度数.
②若![]() ,请探究
,请探究![]() 的值是否为定值,若是,请求出其值;反之,请说明理由
的值是否为定值,若是,请求出其值;反之,请说明理由
【答案】(1)EO⊥FO,EO=FO;理由见解析;(2)①![]() ;②
;②![]() =2
=2
【解析】
(1)由正方形的性质可得BO=CO,∠ABO=∠ACB=45°,∠BOC=90°,由“SAS”可证△BEO≌△CFO,可得OE=OF,∠BOE=∠COF,可证EO⊥FO;
(2)①由等腰直角三角形的性质可得∠EOG的度数;
②由∠EOF=∠ABF=90°,可得点E,点O,点F,点B四点共圆,可得∠EOB=∠BFE,通过证明△BOH∽△BIO,可得![]() ,即可得结论.
,即可得结论.
解:(1)OE=OF,OE⊥OF,连接AC,BD,
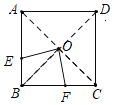
∵点O是正方形ABCD的中心
∴点O是AC,BD的交点
∴BO=CO,∠ABO=∠ACB=45°,∠BOC=90°
∵CF=BE,∠ABO=∠ACB,BO=CO,
∴△BEO≌△CFO(SAS)
∴OE=OF,∠BOE=∠COF
∵∠COF+∠BOF=90°,
∴∠BOE+∠BOF=90°
∴∠EOF=90°,
∴EO⊥FO.
(2)
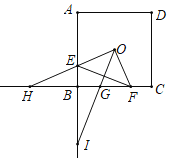
①∵OE=OF,OE⊥OF,
∴△EOF是等腰直角三角形,OG⊥EF
∴∠EOG=45°
②BHBI的值是定值,
理由如下:
如图,连接DB,
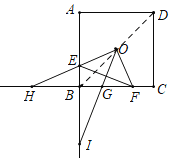
∵AB=BC=CD=2
∴BD=2![]() ,
,
∴BO=![]()
∵∠AOB=∠COB=45°,∠HBE=∠GBI=90°
∴∠HBO=∠IBO=135°
∵∠EOF=∠ABF=90°
∴点E,点O,点F,点B四点共圆
∴∠EOB=∠BFE,
∵EF⊥OI,AB⊥HF
∴∠BEF+∠BFE=90°,∠BEF+∠EIO=90°
∴∠BFE=∠BIO,
∴∠BOE=∠BIO,且∠HBO=∠IBO
∴△BOH∽△BIO
∴![]()
∴BHBI=BO2=2


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
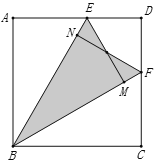
【题目】如图,正方形ABCD的边长为![]() ,点E、F分别为边AD、CD上一点,将正方形分别沿BE、BF折叠,点A的对应点M恰好落在BF上,点C的对应点N恰好落在BE上,则图中阴影部分的面积为_________.
,点E、F分别为边AD、CD上一点,将正方形分别沿BE、BF折叠,点A的对应点M恰好落在BF上,点C的对应点N恰好落在BE上,则图中阴影部分的面积为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O为原点,A、B为数轴上两点,AB=15,且OA:OB=2:1,点P从点B以每秒4个单位的速度向右运动.
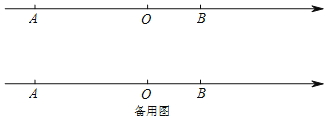
(1)A、B对应的数分别为 、 ;
(2)当点P运动时,分别取BP的中点E,AO的中点F,请画图,并求出![]() 的值;
的值;
(3)若当点P开始运动时,点A、B分别以每秒2个单位和每秒5个单位的速度同时向右运动,是否存在常数m,使得3AP+2OP﹣mBP为定值?若存在,请求出m的值以及这个定值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,E是BC边的中点,连接DE并延长交AB的延长线于点F,则在题中条件下,下列结论不能成立的是( )
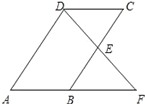
A. BE=CE B. AB=BF C. DE=BE D. AB=DC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点![]() 在数轴上对应的数为
在数轴上对应的数为![]() ,点
,点![]() 对应的数为
对应的数为![]() ,关于
,关于![]() ,
,![]() 的多项式
的多项式![]() 是6次多项式,且常数项为-6.
是6次多项式,且常数项为-6.
(1)点![]() 到
到![]() 的距离为______(直接写出结果);
的距离为______(直接写出结果);
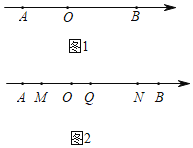
(2)如图1,点![]() 是数轴上一点,点
是数轴上一点,点![]() 到
到![]() 的距离是
的距离是![]() 到
到![]() 的距离的3倍(即
的距离的3倍(即![]() ),求点
),求点![]() 在数轴上对应的数;
在数轴上对应的数;
(3)如图2,点![]() ,
,![]() 分别从点
分别从点![]() ,
,![]() 同时出发,分别以
同时出发,分别以![]() ,
,![]() 的速度沿数轴负方向运动(
的速度沿数轴负方向运动(![]() 在
在![]() ,
,![]() 之间,
之间,![]() 在
在![]() ,
,![]() 之间),运动时间为
之间),运动时间为![]() ,点
,点![]() 为
为![]() ,
,![]() 之间一点,且点
之间一点,且点![]() 到
到![]() 的距离是点
的距离是点![]() 到
到![]() 距离的一半(即
距离的一半(即![]() ),若
),若![]() ,
,![]() 运动过程中
运动过程中![]() 到
到![]() 的距离(即
的距离(即![]() )总为一个固定的值,求
)总为一个固定的值,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)下面的图形是由边长为l的正方形按照某种规律排列而组成的.
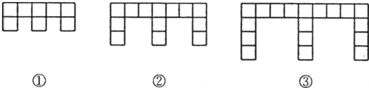
(1)观察图形,填写下表:
图形 | ① | ② | ③ |
正方形的个数 | 8 |
|
|
图形的周长 | 18 |
|
|
(2)推测第n个图形中,正方形的个数为 ,周长为 (都用含n的代数式表示).
(3)这些图形中,任意一个图形的周长y与它所含正方形个数x之间的关系可表示为y= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com