
【题目】如图,已知四边形ABCD和直线MN,点O在直线MN上.
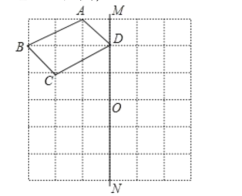
(1)画出四边形![]() 使四边形
使四边形![]() 与四边形ABCD关于直线MN成轴对称;
与四边形ABCD关于直线MN成轴对称;
(2)画出四边形![]() 使四边形
使四边形![]() 与四边形ABCD关于点O对称:
与四边形ABCD关于点O对称:
(3)四边形![]() 和四边形
和四边形![]() 是轴对称和中心对称吗?若是,请在图上画出对称轴或对称中心.
是轴对称和中心对称吗?若是,请在图上画出对称轴或对称中心.
科目:初中数学 来源: 题型:
【题目】如图,点O为原点,A、B为数轴上两点,AB=15,且OA:OB=2:1,点P从点B以每秒4个单位的速度向右运动.
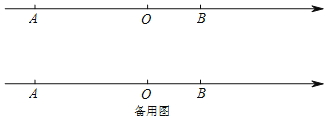
(1)A、B对应的数分别为 、 ;
(2)当点P运动时,分别取BP的中点E,AO的中点F,请画图,并求出![]() 的值;
的值;
(3)若当点P开始运动时,点A、B分别以每秒2个单位和每秒5个单位的速度同时向右运动,是否存在常数m,使得3AP+2OP﹣mBP为定值?若存在,请求出m的值以及这个定值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点![]() 在数轴上对应的数为
在数轴上对应的数为![]() ,点
,点![]() 对应的数为
对应的数为![]() ,关于
,关于![]() ,
,![]() 的多项式
的多项式![]() 是6次多项式,且常数项为-6.
是6次多项式,且常数项为-6.
(1)点![]() 到
到![]() 的距离为______(直接写出结果);
的距离为______(直接写出结果);
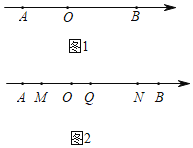
(2)如图1,点![]() 是数轴上一点,点
是数轴上一点,点![]() 到
到![]() 的距离是
的距离是![]() 到
到![]() 的距离的3倍(即
的距离的3倍(即![]() ),求点
),求点![]() 在数轴上对应的数;
在数轴上对应的数;
(3)如图2,点![]() ,
,![]() 分别从点
分别从点![]() ,
,![]() 同时出发,分别以
同时出发,分别以![]() ,
,![]() 的速度沿数轴负方向运动(
的速度沿数轴负方向运动(![]() 在
在![]() ,
,![]() 之间,
之间,![]() 在
在![]() ,
,![]() 之间),运动时间为
之间),运动时间为![]() ,点
,点![]() 为
为![]() ,
,![]() 之间一点,且点
之间一点,且点![]() 到
到![]() 的距离是点
的距离是点![]() 到
到![]() 距离的一半(即
距离的一半(即![]() ),若
),若![]() ,
,![]() 运动过程中
运动过程中![]() 到
到![]() 的距离(即
的距离(即![]() )总为一个固定的值,求
)总为一个固定的值,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,A、B为x轴上两点,C、D为y轴上的两点,经过点A、C、B的抛物线的一部分c1与经过点A、D、B的抛物线的一部分c2组合成一条封闭曲线,我们把这条封闭曲线成为“蛋线”.已知点C的坐标为(0,﹣![]() ),点M是抛物线C2:y=mx2﹣2mx﹣3m(m<0)的顶点.
),点M是抛物线C2:y=mx2﹣2mx﹣3m(m<0)的顶点.
(1)求A、B两点的坐标;
(2)“蛋线”在第四象限上是否存在一点P,使得△PBC的面积最大?若存在,求出△PBC面积的最大值;若不存在,请说明理由;
(3)当△BDM为直角三角形时,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游泳馆普通票价20元![]() 张,暑假为了促销,新推出两种优惠卡:
张,暑假为了促销,新推出两种优惠卡:
![]() 金卡售价600元
金卡售价600元![]() 张,每次凭卡不再收费.
张,每次凭卡不再收费.
![]() 银卡售价150元
银卡售价150元![]() 张,每次凭卡另收10元.
张,每次凭卡另收10元.
暑假普通票正常出售,两种优惠卡仅限暑假使用,不限次数![]() 设游泳x次时,所需总费用为y元
设游泳x次时,所需总费用为y元
![]() 分别写出选择银卡、普通票消费时,y与x之间的函数关系式;
分别写出选择银卡、普通票消费时,y与x之间的函数关系式;
![]() 在同一坐标系中,若三种消费方式对应的函数图象如图所示,请求出点A、B、C的坐标;
在同一坐标系中,若三种消费方式对应的函数图象如图所示,请求出点A、B、C的坐标;
![]() 请根据函数图象,直接写出选择哪种消费方式更合算.
请根据函数图象,直接写出选择哪种消费方式更合算.
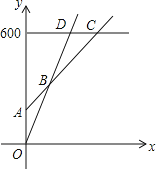
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)下面的图形是由边长为l的正方形按照某种规律排列而组成的.
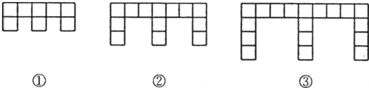
(1)观察图形,填写下表:
图形 | ① | ② | ③ |
正方形的个数 | 8 |
|
|
图形的周长 | 18 |
|
|
(2)推测第n个图形中,正方形的个数为 ,周长为 (都用含n的代数式表示).
(3)这些图形中,任意一个图形的周长y与它所含正方形个数x之间的关系可表示为y= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两地相距300千米,一辆货车和一辆轿车分别从甲地开往乙地![]() 轿车的平均速度大于货车的平均速度
轿车的平均速度大于货车的平均速度![]() ,如图,线段OA、折线BCD分别表示两车离甲地的距离
,如图,线段OA、折线BCD分别表示两车离甲地的距离![]() 单位:千米
单位:千米![]() 与时间
与时间![]() 单位:小时
单位:小时![]() 之间的函数关系.
之间的函数关系.
![]() 线段OA与折线BCD中,______表示货车离甲地的距离y与时间x之间的函数关系.
线段OA与折线BCD中,______表示货车离甲地的距离y与时间x之间的函数关系.
![]() 求线段CD的函数关系式;
求线段CD的函数关系式;
![]() 货车出发多长时间两车相遇?
货车出发多长时间两车相遇?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com