
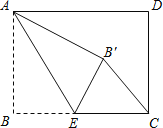
【题目】如图,矩形ABCD中,![]() ,点E是BC边上一点,连接AE,把
,点E是BC边上一点,连接AE,把![]() 沿AE折叠,使点B落在点
沿AE折叠,使点B落在点![]() 处
处![]() 当
当![]() 为直角三角形时,BE的长为______.
为直角三角形时,BE的长为______.
【答案】![]() 或3
或3
【解析】分析:当△CEB′为直角三角形时,有两种情况:
①当点B′落在矩形内部时,如答图1所示.
连结AC,先利用勾股定理计算出AC=5,根据折叠的性质得∠AB′E=∠B=90°,而当△CEB′为直角三角形时,只能得到∠EB′C=90°,所以点A、B′、C共线,即∠B沿AE折叠,使点B落在对角线AC上的点B′处,则EB=EB′,AB=AB′=3,可计算出CB′=2,设BE=x,则EB′=x,CE=4﹣x,然后在Rt△CEB′中运用勾股定理可计算出x.
②当点B′落在AD边上时,如答图2所示.此时ABEB′为正方形.
详解:当△CEB′为直角三角形时,有两种情况:

①当点B′落在矩形内部时,如答图1所示.
连结AC.在Rt△ABC中,AB=3,BC=4,∴AC=![]() =5.∵∠B沿AE折叠,使点B落在点B′处,∴∠AB′E=∠B=90°,当△CEB′为直角三角形时,只能得到∠EB′C=90°,∴点A、B′、C共线,即∠B沿AE折叠,使点B落在对角线AC上的点B′处,∴EB=EB′,AB=AB′=3,∴CB′=5﹣3=2,设BE=x,则EB′=x,CE=4﹣x.在Rt△CEB′中,∵EB′2+CB′2=CE2,∴x2+22=(4﹣x)2,解得:x=
=5.∵∠B沿AE折叠,使点B落在点B′处,∴∠AB′E=∠B=90°,当△CEB′为直角三角形时,只能得到∠EB′C=90°,∴点A、B′、C共线,即∠B沿AE折叠,使点B落在对角线AC上的点B′处,∴EB=EB′,AB=AB′=3,∴CB′=5﹣3=2,设BE=x,则EB′=x,CE=4﹣x.在Rt△CEB′中,∵EB′2+CB′2=CE2,∴x2+22=(4﹣x)2,解得:x=![]() ,∴BE=
,∴BE=![]() ;
;
②当点B′落在AD边上时,如答图2所示.
此时ABEB′为正方形,∴BE=AB=3.
综上所述:BE的长为![]() 或3.
或3.
故答案为:![]() 或3.
或3.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
【题目】某校为了解学生的课外阅读情况,对部分学生进行了调查,并统计他们平均每天的课外阅读时间t(单位:min),然后利用所得数据绘制如下两幅不完整的统计图.
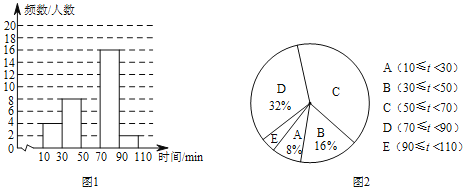
请你根据以上信息解答下列问题:
(1)本次调查活动采取了 调查方式,样本容量是 .
(2)图2中C的圆心角度数为 度,补全图1的频数分布直方图.
(3)该校有900名学生,估计该校学生平均每天的课外阅读时间不少于50min的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把正整数1,2,3,…,2018排成如图所示的7列,规定从上到下依次为第1行、第2行、第3行、…,从左到右依次为第1至7列.
(1)数2018在第______行第______列;
(2)按如图所示的方法用方框框出四个数,这四个数的和能否为296?如果能,求出这四个数;如果不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新能源汽车环保节能,越来越受到消费者的喜爱.各种品牌相继投放市场.一汽贸公司经销某品牌新能源汽车.去年销售总额为5000万元,今年1~5月份,每辆车的销售价格比去年降低1万元.销售数量与去年一整年的相同.销售总额比去年一整年的少20%,今年1~5月份每辆车的销售价格是多少万元?设今年1~5月份每辆车的销售价格为x万元.根据题意,列方程正确的是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD和直线MN,点O在直线MN上.
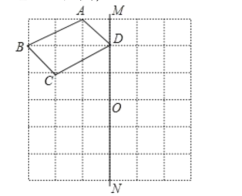
(1)画出四边形![]() 使四边形
使四边形![]() 与四边形ABCD关于直线MN成轴对称;
与四边形ABCD关于直线MN成轴对称;
(2)画出四边形![]() 使四边形
使四边形![]() 与四边形ABCD关于点O对称:
与四边形ABCD关于点O对称:
(3)四边形![]() 和四边形
和四边形![]() 是轴对称和中心对称吗?若是,请在图上画出对称轴或对称中心.
是轴对称和中心对称吗?若是,请在图上画出对称轴或对称中心.
查看答案和解析>>
科目:初中数学 来源: 题型:
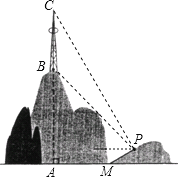
【题目】如图,山顶建有一座铁塔,塔高![]() 米,测量人员在一个小山坡的P处测得塔的底部B点的仰角为
米,测量人员在一个小山坡的P处测得塔的底部B点的仰角为![]() ,塔顶C点的仰角为
,塔顶C点的仰角为![]() 已测得小山坡的坡角为
已测得小山坡的坡角为![]() ,坡长
,坡长![]() 米
米![]() 求山的高度
求山的高度![]() 精确到1米
精确到1米![]() 参考数据:
参考数据:![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,矩形ABCD中,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.
(1)如图1,连接AF、CE,求证:四边形AFCE为菱形;
(2)如图2,若AB=4cm,AF=5cm,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周,即点P自A→F→B→A停止,点Q自C→D→E→C停止,在运动过程中:
①已知点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为![]() 秒,当A、C、P、Q四点为顶点的四边形是平行四边形时,求
秒,当A、C、P、Q四点为顶点的四边形是平行四边形时,求![]() 的值;
的值;
②若点P、Q的运动路程分别为![]() (单位:cm,
(单位:cm,![]() ),已知A、C、P、Q四点为顶点的四边形是平行四边形,求
),已知A、C、P、Q四点为顶点的四边形是平行四边形,求![]() 与
与![]() 满足的数量关系式。
满足的数量关系式。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若干名工人某天生产同一种玩具,生产的玩具数整理成条形图(如图所示).则他们生产的玩具数的平均数、中位数、众数分别为( )

A.5,5,4 B.5,5,5
C.5,4,5 D.5,4,4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com