
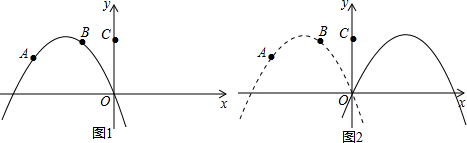
分析 (1)将点A、点B的坐标代入抛物线C1解析式,求得a与k的值即可求得其解析式;(2)在抛物线C1上找出与点B到直线OA的距离相等的点即可;(3)根据相似三角形的判定:两组对应边的比值相等且夹角也相等的两三角形相似,或:平行于三角形一边的直线截三角形的两边(或两边的延长线)所得的三角形与原三角形相似,求得相应的点Q的坐标即可.
解答 解:(1)∵抛物线过点A(-5,$\frac{15}{8}$)和点B(-2,3),
∴$\left\{\begin{array}{l}{a(-5+3)^{2}+k=\frac{15}{8}}\\{a(-2+3)^{2}+k=3}\end{array}\right.$
∴$\left\{\begin{array}{l}{a=-\frac{3}{8}}\\{k=\frac{27}{8}}\end{array}\right.$
∴抛物线C1的解析式为y=-$\frac{3}{8}(x+3)^{2}+\frac{27}{8}$
(2)直线OA:y=-$\frac{3}{8}$x,则过B平行于OA的直线BE:y=-$\frac{3}{8}x+\frac{9}{4}$,
设抛物线C1与直线BE交于点P(x,y),
$\left\{\begin{array}{l}{y=-\frac{3}{8}{x}^{2}-\frac{9}{4}x}\\{y=-\frac{3}{8}x+\frac{9}{4}}\end{array}\right.$
解得 $\left\{\begin{array}{l}{{x}_{1}=-2}\\{{y}_{1}=3}\end{array}\right.$(舍去)$\left\{\begin{array}{l}{{x}_{2}=-3}\\{{y}_{2}=\frac{27}{8}}\end{array}\right.$
∴${P}_{1}(-3,\frac{27}{8})$.
直线BE交y轴于点E,则E关于x轴的对称点为F$(0,\frac{9}{4})$,
∴过F平行于OA的直线MF:y=-$\frac{3}{8}x-\frac{9}{4}$,
设抛物线C1与直线MF交于点P(x,y),
$\left\{\begin{array}{l}{y=-\frac{3}{8}{x}^{2}-\frac{9}{4}x}\\{y=-\frac{3}{8}x-\frac{9}{4}}\end{array}\right.$
解得$\left\{\begin{array}{l}{{x}_{1}=-6}\\{{y}_{1}=0}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=1}\\{{y}_{2}=-\frac{21}{8}}\end{array}\right.$.
∴P2(-6,0),${P}_{3}(1,-\frac{21}{8})$.
(3)抛物线C1向右平移6个单位后所得抛物线C2:y=-$\frac{3}{8}(x-3)^{2}+\frac{27}{8}$,
点B平移后得点D(4,3),
∵C(0,3),D(4,3),
∴CD∥x轴.
抛物线C2的对称轴为:直线x=3交x轴于Q1(3,0).
过O垂直于OM的直线交对称轴于Q2,
则有$O{{Q}_{1}}^{2}=M{Q}_{1}•{Q}_{1}{Q}_{2}$,
直线OD:y=$\frac{3}{4}x$交对称轴于M(3,$\frac{9}{4}$),
∴Q2(3,-4)
综上所述,满足要求的点Q的坐标为(3,0)或(3,-4).
点评 此题考查了垂径定理、用待定系数法求函数解析式和函数交点坐标与方程组的解的关系,(3)是结论开放性题目,需要进行探索,解题时要分析满足条件的不同情况,不可漏解.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,学校有一块长为(3a+b)米,宽为(2a+b)米的长方形地块,计划将阴影部分进行绿化,中间将修建一座雕像,则绿化的面积是多少平方米?(用a、b关系式表示)
如图,学校有一块长为(3a+b)米,宽为(2a+b)米的长方形地块,计划将阴影部分进行绿化,中间将修建一座雕像,则绿化的面积是多少平方米?(用a、b关系式表示)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | πcm2 | B. | 2πcm2 | C. | 3πcm2 | D. | 6πcm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
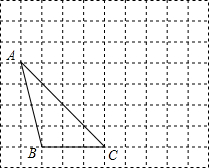 在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,将△ABC先向右平移5个单位得△A1B1C1,再向上平移2个单位得△A2B2C2.
在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,将△ABC先向右平移5个单位得△A1B1C1,再向上平移2个单位得△A2B2C2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com