练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    △ABC中，BF、CF是角平分线，∠A=70°，则∠BFC=（　　）
    A、125°B、110°
    C、100°D、150°
    考点：三角形内角和定理
    专题：
    分析：根据三角形的内角和定理和∠A的度数求得另外两个内角的和，利用角平分线的性质得到这两个角和的一半，用三角形内角和减去这两个角的一半即可．
    解答：解：∵∠A=70°，
    ∴∠ABC+∠ACB=180°-∠A=180°-70°=110°，
    ∵BF、CF是△ABC的角平分线，
    ∴∠FBC+∠FCB=
    1
    2
    （∠ABC+∠ACB）=55°，
    ∴∠BFC=180°-55°=125°．
    故选：A．
    点评：本题考查了三角形的内角和定理与角平分线的性质，掌握三角形的内角和定理是解决问题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    如图，直线AB，CD相交于点E，FE⊥AB，若∠FEC-∠AEC=20°，那么∠AED的度数是
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    a、b两数在一条隐去原点的数轴上的位置如图所示，①a-b＜0；②a+b＜0；③ab＜0；④（a+1）（b+1）＜0，上述4个式子中一定成立的是
     
    （只填写序号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

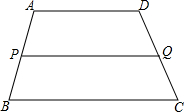    如图，在梯形ABCD中，AD∥BC，P是AB的中点，过P点作AD的平行线交DC于Q点．
    （1）线段PQ与BC平行吗？为什么？
    （2）测量并回答：DQ与CQ是否相等？
    （3）通过测量并判断：
    1
    2
    (AD+BC)=PQ    是否成立？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    为了了解南山区学生喜欢球类活动的情况，采取抽样调查的方法，从足球、乒乓球、篮球、排球等四个方面调查了全班学生的兴趣爱好，根据调查的结果绘制成如图所示的两幅不完整的统计图（如图①，②，要求每位学生只能选择一种自己喜欢的球类），请你根据图中提供的信息解答下列问题：
    （1）本次共调查的学生人数为
     
    ，并把条形统计图补充完整；
    （2）扇形统计图中m=
     
    ，n=
     
    ；
    （3）表示“足球”的扇形的圆心角是
     
    度；
    （4）若南山区初中学生共有60000人，则喜欢乒乓球的有多少人？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    将平面直角坐标系平移，使原点O移至点A（4，-1），这时在新坐标系中原来点O的坐标是
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    下列等式的变形错误的是（　　）
    A、由a=b得a+5=b+5
    B、由a=b得
    a
    9
    =
    b
    9
    C、由x+2=y+2得x=y
    D、由-3x=-3y得x=-y

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，点D在△ABC的边AC上，添加下列一个条件仍不能判断△ADB与△ABC相似的是（　　）
    A、∠ABD=∠C
    B、∠ADB=∠ABC
    C、BC2=CD•AC
    D、AB2=AD•AC

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    给窗户装遮阳棚，其目的为最大限度地遮挡夏天炎热的阳光，又能最大限度地使冬天温暖的阳光射入室内，现请你为我校新建成的高中部教学楼朝南的窗户设计一个直角形遮阳蓬BCD，如图，已知窗户AB高度为h=2米，本地冬至日正午时刻太阳光与地面的最小夹角α=32°，夏至日正午时刻太阳光与地面的最大夹角β=79°，请分别计算直角形遮阳蓬BCD中BC、CD的长（结果精确到0.1米）

    查看答案和解析>>

    同步练习册答案