
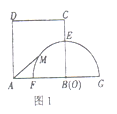
【题目】如图1,四边形![]() 是正方形,且
是正方形,且![]() ,点
,点![]() 与
与![]() 重合,以
重合,以![]() 为圆心,作半径长为5的半圆
为圆心,作半径长为5的半圆![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .
.
发现![]() 是半圆
是半圆![]() 上任意一点,连接
上任意一点,连接![]() ,则
,则![]() 的最大值为______;
的最大值为______;
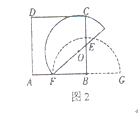
思考如图2,将半圆![]() 绕点
绕点![]() 逆时针旋转,记旋转角为
逆时针旋转,记旋转角为![]()
(1)当![]() 时,求半圆
时,求半圆![]() 落在正方形内部的弧长;
落在正方形内部的弧长;
(2)在旋转过程中,若半圆![]() 与正方形
与正方形![]() 的边相切时,请直接写出此时点
的边相切时,请直接写出此时点![]() 到切点的距离.(注:
到切点的距离.(注:![]() ,
,![]() ,
,![]() )
)
【答案】发现: 13;思考:(1)![]() ;(2)点A到切点的距离为3或
;(2)点A到切点的距离为3或![]() 或
或![]() .
.
【解析】
发现:当点M与点G重合时,AM的值最大,据此求解即可;
思考:(1)设半圆O交AD于点N,连接ON,过点O作OH⊥AD于点H.先证明四边形HAFO是矩形,从而AH∥OF,根据锐角三角函数的定义求解即可出∠NOF和∠HNO的值,然后根据弧长公式计算即可;
(2)分三种情况求解,①半圆O与AB相切时,②半圆O与CD相切时,③当半圆O与AD相切时.
解:发现 当点M与点G重合时,AM的值最大,最大值为8+5=13.
思考 (1)如图①,设半圆O交AD于点N,连接ON,过点O作OH⊥AD于点H.
∵四边形ABCD是正方形,∴∠DAB=90°.
∵半圆O绕点F逆时针旋转90°,∴∠OFA=90°.
∴四边形HAFO是矩形.
∴AH=OF,OH=AF=AB-BF=3, AH∥OF.
∴sin∠HNO=![]() =
=![]() . ∴∠HNO=37°.
. ∴∠HNO=37°.
∴∠NOF=∠HNO=37°.
∴半圆O落在正方形内部的弧NF的长=![]() ;
;
(2)点A到切点的距离为3或![]() 或
或![]() .
.
∵由(1)知,当α=90°时,半圆O与AB相切,此时切点为点F,
∴AF=3;
如图②,当半圆O与CD相切时,设切点为R,连接OR,AR,并延长RO交AB于点T,
∴∠ORC=90°.
∵DC∥AB,
∴∠OTF=90°.
∴四边形RCBT是矩形.
∴RT=CB=8.
∴OT=8-5=3.
∴FT=![]() =4, AT=AB-BT=AB-(BF-FT)=7.
=4, AT=AB-BT=AB-(BF-FT)=7.
∴AR=![]() =
=![]() ;
;
∴如图③,当半圆O与AD相切时,设切点为P,连接OP,过点F作FS⊥PO于点S,易得四边形PAFS是矩形,
∴PS=AF=3, AP=SF.
∴SO=PO-PS=53=2.
∴SF=![]() =
=![]() .
.
∴AP=SF=![]() .
.
综上,点A到切点的距离为3或![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】已知某种商品的进价为每件30元该商品在第x天的售价是y1(单位:元/件),销量是y2(单位:件),且满足关系式![]() ,y2=200﹣2x,设每天销售该商品的利润为w元.
,y2=200﹣2x,设每天销售该商品的利润为w元.
(1)写出w与x的函数关系式;
(2)销售该商品第几天时,当天销售利润最大?最大利润是多少?
(3)该商品销售过程中,共有多少天日销售利润不低于4800元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南.北两个园林场去年共有员工500人,其中南园林场员工数比北园林场员工数的2倍少100人.
(1)求去年南.北两个园林场的员工数;
(2)经核算,去年南园林场年产值比北园林场年产值少m%.北园林场人均产值比南园林场人均产值多4m%,且两个园林场人均产值不低于北园林场人均产值的![]() .求m的值.
.求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 边的高,点
边的高,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴上,点
轴上,点![]() 在第一象限,若
在第一象限,若![]() 从原点出发,沿
从原点出发,沿![]() 轴向右以每秒1个单位长的速度运动,则点
轴向右以每秒1个单位长的速度运动,则点![]() 随之沿
随之沿![]() 轴下滑,并带动
轴下滑,并带动![]() 在平面内滑动,设运动时间为
在平面内滑动,设运动时间为![]() 秒,当
秒,当![]() 到达原点时停止运动
到达原点时停止运动
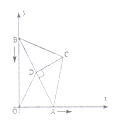
(1)连接![]() ,线段
,线段![]() 的长随
的长随![]() 的变化而变化,当
的变化而变化,当![]() 最大时,
最大时,![]() ______.
______.
(2)当![]() 的边与坐标轴平行时,
的边与坐标轴平行时,![]() ______.
______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 交
交![]() 轴于点
轴于点![]() (
(![]() 在
在![]() 的左侧),交
的左侧),交![]() 轴于点
轴于点![]() ,点
,点![]() 为线段
为线段![]() 上一点,过点
上一点,过点![]() 作
作![]() 轴交抛物线于点
轴交抛物线于点![]() ,过点
,过点![]() 作
作![]() 轴交抛物线于点
轴交抛物线于点![]() . 设点
. 设点![]() 的横坐标为
的横坐标为![]() .
.
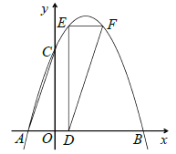
(1)当![]() 时,求
时,求![]() 的长.
的长.
(2)连结![]() ,当
,当![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,CD是弦,AB⊥CD,垂足为E,点P在⊙O上,连接BP、PD、BC.若CD=![]() ,sinP=
,sinP=![]() ,则⊙O的直径为( )
,则⊙O的直径为( )

A. 8 B. 6 C. 5 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
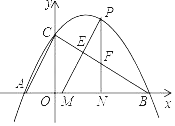
【题目】如图,二次函数y=ax2+bx+![]() 的图象经过A(﹣1,0),B(3,0),与y轴相交于点C.点P为第一象限的抛物线上的一个动点,过点P分别做BC和x轴的垂线,交BC于点E和F,交x轴于点M和N.
的图象经过A(﹣1,0),B(3,0),与y轴相交于点C.点P为第一象限的抛物线上的一个动点,过点P分别做BC和x轴的垂线,交BC于点E和F,交x轴于点M和N.
(1)求这个二次函数的解析式;
(2)求线段PE最大值,并求出线段PE最大时点P的坐标;
(3)若S△PMN=3S△PEF时,求出点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com