已知点A(-1,-1)在抛物线y=(k2-1)x2-2(k-2)x+1(其中x是自变量)上.
(1)求抛物线的对称轴;
(2)若B点与A点关于抛物线的对称轴对称,问是否存在与抛物线只交于一点B的直线?如果存在,求符合条件的直线解析式;如果不存在,说明理由.
【答案】
分析:(1)把点A坐标代入抛物线解析式,计算求出k的值,再根据抛物线对称轴x=-
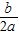
进行计算即可得解;
(2)先根据对称性求出点B的坐标,再分直线过点B且与y轴平行时,与抛物线只有一个交点,直线过点B不与y轴平行时,设直线解析式为y=mx+n,把点B的坐标代入解析式得到一个关于m、n的方程,再与抛物线解析式联立消掉y,得到关于x的一元二次方程,根据只有一个交点,利用根的判别式△=0,列式整理得到一个关于m、n的方程,两个方程联立求解即可得到m、n的值,从而求出直线解析式.
解答:解:(1)已知点A(-1,-1)在已知抛物线上,
则(k
2-1)+2(k-2)+1=-1,
即k
2+2k-3=0,
解得 k
1=1,k
2=-3,…分
当k=1时,函数y=(k
2-1)x
2-2(k-2)x+1为一次函数,不合题意,舍去,
当k=-3时,抛物线的解析式为y=8x
2+10x+1,…(4分)
由抛物线的解析式知其对称轴为x=-

=-
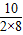
=-

,
即x=-

;…(5分)
(2)存在.
理由如下:∵点B与点A关于y=(k
2-1)x
2-2(k-2)x+1对称,且A(-1,-1),
∴B(-

,-1),…(6分)
当直线过B(-

,-1)且与y轴平行时,此直线与抛物线只有一个交点,
此时的直线为x=-

,…(8分)
当直线过B(-

,-1)且不与y轴平行时,
设直线y=mx+n与抛物线y=8x
2+10x+1只交于一点B,
则-

m+n=-1,…(10分)
即m-4n-4=0,①
把y=mx+n代入y=8x
2+10x+1,得8x
2+10x+1=mx+n,…(11分)
即8x
2+(10-m)x+1-n=0,…(12分)
由8x
2+(10-m)x+1-n=0,△=0,得(10-m)
2-32(1-n)=0,②
由①,②得
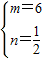
故所求的直线为y=6x+

,
综上所述,存在与抛物线只交于一点B的直线x=-

或y=6x+

.…(14分)
点评:本题考查了二次函数的性质,抛物线的对称轴的求解,抛物线与直线的交点问题,以及根的判别式的应用,本题主要要分情况讨论.

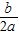 进行计算即可得解;
进行计算即可得解; =-
=-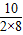 =-
=- ,
, ;…(5分)
;…(5分) ,-1),…(6分)
,-1),…(6分) ,-1)且与y轴平行时,此直线与抛物线只有一个交点,
,-1)且与y轴平行时,此直线与抛物线只有一个交点, ,…(8分)
,…(8分) ,-1)且不与y轴平行时,
,-1)且不与y轴平行时, m+n=-1,…(10分)
m+n=-1,…(10分)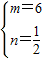
 ,
, 或y=6x+
或y=6x+ .…(14分)
.…(14分)

 2,A3的横坐标依次为三个连续整数,其他条件不变,求线段CA2的长.
2,A3的横坐标依次为三个连续整数,其他条件不变,求线段CA2的长.