【题目】已知BD、CE是△ABC的两条高，直线BD、CE相交于点H．
（1）若∠A=100°，如图，求∠DHE的度数；
（2）若△ABC中∠A=50°，直接写出∠DHE的度数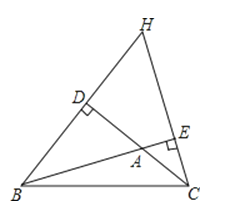
【答案】解：（1）∵BD、CE是△ABC的两条高，
∴∠HDA=∠HEA=90°，
∴∠DHE=180°﹣∠A=80°；
（2）当∠A=50°时，
①△ABC是锐角三角形时，∠DHE=180°﹣50°=130°；
②△ABC是钝角三角形时，∠DHE=∠A=50°；
故答案为：50°或130°．
【解析】（1）根据四边形的内角和是360°，求得∠DHE的度数；
（2）分∠A是锐角时△ABC是锐角三角形，钝角三角形讨论求解即可．
【考点精析】解答此题的关键在于理解三角形的内角和外角的相关知识，掌握三角形的三个内角中，只可能有一个内角是直角或钝角；直角三角形的两个锐角互余；三角形的一个外角等于和它不相邻的两个内角的和；三角形的一个外角大于任何一个和它不相邻的内角．
名师指导期末冲刺卷系列答案
开心蛙口算题卡系列答案科目：初中数学 来源： 题型：
【题目】阅读材料：
小明在学习二次根式后，发现一些含根号的式子可以写成另一个式子的平方，如3+2
=（1+
）2．善于思考的小明进行了以下探索：
设a+b
=（m+n
）2（其中a、b、m、n均为整数），则有a+b
=m2+2n2+2mn
．
∴a=m2+2n2，b=2mn．这样小明就找到了一种把类似a+b
的式子化为平方式的方法．
请你仿照小明的方法探索并解决下列问题：
（1）当a、b、m、n均为正整数时，若a+b
=
，用含m、n的式子分别表示a、b，得：a=__，b=__；
（2）利用所探索的结论，找一组正整数a、b、m、n填空：__+__
=（___）+__
）2；
（3）若a+4
=
，且a、m、n均为正整数，求a的值？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知y是z的一次函数，z是x的正比例函数．
(1)问：y是x的一次函数吗？
(2)若当x＝5时，y＝2；当x＝－3时，y＝6，求当x＝1时y的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，OE平分∠AOB，且EC⊥OA，ED⊥OB，垂足分别是C，D，连结CD与OE交于点F.
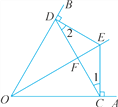
(1)求证：∠1＝∠2.
(2)求证：OE是线段CD的垂直平分线．
(3)若∠1＝30°，OC＝2，求△OCD与△CDE的面积之差．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知OP平分∠AOB，∠AOB=60°，CP=2，CP∥OA，PD⊥OA于点D，PE⊥OB于点E．如果点M是OP的中点，则DM的长是（ ）
A. 2 B. 
C. 
D. 2
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AB∥CD，OE平分∠BOC，OF⊥OE，OP⊥CD，∠ABO=a°，则下列结论：
①∠BOE=
（180﹣a）°；②OF平分∠BOD；③∠POE=∠BOF；④∠POB=2∠DOF．
其中正确的个数有多少个？（ ）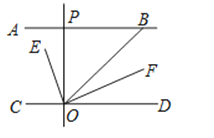
A.1
B.2
C.3
D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
