
已知二次函数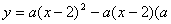 为常数,且
为常数,且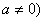 .
.
(1)求证:不论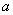 为何值,该函数的图象与
为何值,该函数的图象与 轴总有两个公共点;
轴总有两个公共点;
(2)设该函数的图象的顶点为C,与 轴交于A,B两点,当△ABC
轴交于A,B两点,当△ABC
的面积等于2时,求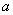 的值.
的值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
如图一艘海上巡逻船在A地巡航,这时接到B地海上指挥中心紧急通知:在指挥中心北偏西60º方向的C地有一艘渔船遇险,要求马上前去救援.此时C地位于A地北偏西30°方向上.A地位于B地北偏调西75°方向上.AB两地之间的距离为12海里.求A.C两地之间的距离. (参考数据: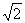 ≈l. 41,
≈l. 41, ≈1.73,
≈1.73,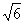 ≈2.45.结果精确到0.1.)
≈2.45.结果精确到0.1.)

查看答案和解析>>
科目:初中数学 来源: 题型:
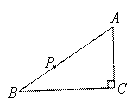
如图,在Rt△ABC中,∠C = 90°,P是斜边上一定点,过点P作直线与一直角边交于点Q,使图中出现两个相似三角形,这样的点Q有
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
已知抛物线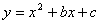 经过(2,-1)和(4 , 3)两点.
经过(2,-1)和(4 , 3)两点.
(1)求出这个抛物线的解析式;
(2)将该抛物线向右平移1个单位,再向下平移3个单位,得到的
新抛物线解析式为  .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
(1)在Rt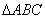 中,∠C = 90°, ∠B = 30°.
中,∠C = 90°, ∠B = 30°.
①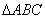 绕点C顺时针旋转得到
绕点C顺时针旋转得到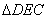 ,点
,点 恰好落在
恰好落在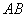 边上.如图1,则
边上.如图1,则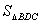 与
与 的数量关系是 ;
的数量关系是 ;
②当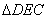 绕点C旋转到图2的位置时,小娜猜想①中
绕点C旋转到图2的位置时,小娜猜想①中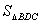 与
与 的数量关系仍然成立,并尝试分别作出了
的数量关系仍然成立,并尝试分别作出了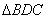 和
和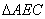 中BC,C
中BC,C 边上的高,请你证明小娜的猜想;[来源:学_科_网]
边上的高,请你证明小娜的猜想;[来源:学_科_网]
(2)已知,∠ABC = 60°,点 是∠ABC平分线上一点,
是∠ABC平分线上一点,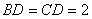 ,
, 交
交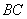 于点
于点 ,如图3.若在射线
,如图3.若在射线 上存在点
上存在点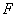 ,使
,使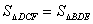 ,则
,则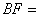
 .
.



1 图2  图3
图3
查看答案和解析>>
科目:初中数学 来源: 题型:
若关于x的方程(m2-1)x2-(m+1)x+8=0是一元一次方程 ,有四位学生求得m的值分别如下:①m=±1;②m=1;③m=-1;④m=0.其中错误的个数是( ).
,有四位学生求得m的值分别如下:①m=±1;②m=1;③m=-1;④m=0.其中错误的个数是( ).
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
如图所示,一扇窗户打开后,用窗钩AB即可固定,这里所用的几何原理是( ).

A.两点之间线段最短 B.垂线段最短
C.两定确定一条直线 D.三角形的稳定性
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com