
【题目】已知点P是线段AB上与点A不重合的一点,且AP<PB.AP绕点A逆时针旋转角α(0°<α≤90°)得到AP1 , BP绕点B顺时针也旋转角α得到BP2 , 连接PP1、PP2 . 
(1)如图1,当α=90°时,求∠P1PP2的度数;
(2)如图2,当点P2在AP1的延长线上时,求证:△P2P1P∽△P2PA;
(3)如图3,过BP的中点E作l1⊥BP,过BP2的中点F作l2⊥BP2 , l1与l2交于点Q,连接PQ,求证:P1P⊥PQ.
【答案】
(1)
解:由旋转的性质得:AP=AP1,BP=BP2.
∵α=90°,
∴△PAP1和△PBP2均为等腰直角三角形,
∴∠APP1=∠BPP2=45°,
∴∠P1PP2=180°﹣∠APP1﹣∠BPP2=90°.
(2)
解:
证明:由旋转的性质可知△PAP1和△PBP2均为顶角为α的等腰三角形,
∴∠APP1=∠BPP2=90°﹣![]() ,
,
∴∠P1PP2=180°﹣(∠APP1+∠BPP2)=180°﹣2(90°﹣![]() )=α,
)=α,
在△PP2P1和△P2PA中,∠P1PP2=∠PAP2=α,
又∵∠PP2P1=∠AP2P,
∴△P2P1P∽△P2PA.
(3)
解:证明:如图,连接QB.
∵l1,l2分别为PB,P2B的中垂线,
∴EB=![]() BP,FB=
BP,FB=![]() BP2.
BP2.
又BP=BP2,
∴EB=FB.
在Rt△QBE和Rt△QBF中,
![]() ,
,
∴Rt△QBE≌Rt△QBF,
∴∠QBE=∠QBF=![]() ∠PBP2=
∠PBP2=![]() ,
,
由中垂线性质得:QP=QB,
∴∠QPB=∠QBE=![]() ,
,
由(2)知∠APP1=90°﹣![]() ,
,
∴∠P1PQ=180°﹣∠APP1﹣∠QPB=180°﹣(90°﹣![]() )﹣
)﹣![]() =90°,
=90°,
即 P1P⊥PQ.

【解析】(1)利用旋转的性质以及等腰直角三角形得出∠APP1=∠BPP2=45°,进而得出答案;
(2)根据题意得出△PAP1和△PBP2均为顶角为α的等腰三角形,进而得出∠P1PP2=∠PAP2=α,求出△P2P1P∽△P2PA;
(3)首先连结QB,得出Rt△QBE≌Rt△QBF,利用∠P1PQ=180°﹣∠APP1﹣∠QPB求出即可.
【考点精析】利用相似三角形的判定与性质对题目进行判断即可得到答案,需要熟知相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A(﹣1,m)在直线y=2x+3上,连结OA,将线段OA绕点O顺时针旋转90°,点A的对应点B恰好落在直线y=﹣x+b上,则b的值为( )
A.-2
B.1
C.![]() ?
?
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】任意大于1的正整数m的三次幂均可“分裂”成m个连续奇数的和,如:23=3+5,33=7+9+11,43=13+15+17+19,…按此规律,若m3分裂后其中有一个奇数是2015,则m的值是( )
A.46
B.45
C.44
D.43
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+2x+c的图象与x轴交于点A(﹣1,0)和点B,与y轴交于点C(0,3).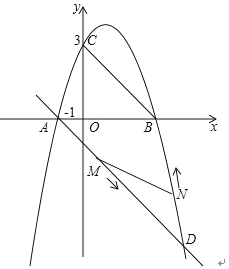
(1)求该二次函数的表达式;
(2)过点A的直线AD∥BC且交抛物线于另一点D,求直线AD的函数表达式;
(3)在(2)的条件下,请解答下列问题:
①在x轴上是否存在一点P,使得以B、C、P为顶点的三角形与△ABD相似?若存在,求出点P的坐标;若不存在,请说明理由;
②动点M以每秒1个单位的速度沿线段AD从点A向点D运动,同时,动点N以每秒![]() 个单位的速度沿线段DB从点D向点B运动,问:在运动过程中,当运动时间t为何值时,△DMN的面积最大,并求出这个最大值.
个单位的速度沿线段DB从点D向点B运动,问:在运动过程中,当运动时间t为何值时,△DMN的面积最大,并求出这个最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】湘西自治州风景优美,物产丰富,一外地游客到某特产专营店,准备购买精加工的豆腐乳和猕猴桃果汁两种盒装特产.若购买3盒豆腐乳和2盒猕猴桃果汁共需180元;购买1盒豆腐乳和3盒猕猴桃果汁共需165元.
(1)请分别求出每盒豆腐乳和每盒猕猴桃果汁的价格;
(2)该游客购买了4盒豆腐乳和2盒猕猴桃果汁,共需多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】假如娄底市的出租车是这样收费的:起步价所包含的路程为0~1.5千米,超过1.5千米的部分按每千米另收费.
小刘说:“我乘出租车从市政府到娄底汽车站走了4.5千米,付车费10.5元.”
小李说:“我乘出租车从市政府到娄底汽车站走了6.5千米,付车费14.5元.”
问:
(1)出租车的起步价是多少元?超过1.5千米后每千米收费多少元?
(2)小张乘出租车从市政府到娄底南站(高铁站)走了5.5千米,应付车费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C、D为半圆O的三等分点,过点C作CE⊥AD,交AD的延长线于点E.
(1)求证:CE是⊙O的切线;
(2)判断四边形AOCD是否为菱形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C为⊙O上一点,AE和过点C的切线互相垂直,垂足为E,AE交⊙O于点D,直线EC交AB的延长线于点P,连接AC,BC,PB:PC=1:2.
(1)求证:AC平分∠BAD;
(2)探究线段PB,AB之间的数量关系,并说明理由;
(3)若AD=3,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com