
【题目】如图,AD是△ABC的边BC上的高,添加下列条件中的某一个,不能推出△ABC为等腰三角形的是( )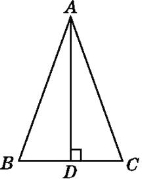
A.∠BAD=∠ACD
B.∠BAD=∠CAD
C.BD=CD
D.∠B=∠C
【答案】A
【解析】解 :①如果添加∠BAD=∠CAD;能推出△ABC为等腰三角形,理由如下:
∵ AD⊥BC ,
∴∠ADB=∠ADC=90° ,
又∵AD=AD, ∠BAD=∠CAD ,
∴ △ADC≌△ADB (ASA)
∴ AB=AC ,
∴ △ABC是等腰三角形;
故B不符合题意;
②如果添加BD=CD;能推出△ABC为等腰三角形,理由如下:
∵ AD⊥BC ,
∴∠ADB=∠ADC=90°
又∵AD=AD, BD=CD
∴ △ADC≌△ADB (SAS)
∴ AB=AC ,
∴ △ABC是等腰三角形;
故C不符合题意;
③如果添加∠B=∠C;能推出△ABC为等腰三角形,理由如下:
∵ AD⊥BC ,
∴∠ADB=∠ADC=90°
又∵AD=AD, ∠B=∠C;
∴ △ADC≌△ADB (AAS)
∴ AB=AC ,
∴ △ABC是等腰三角形;
故D不符合题意;
综上所述只有A符合题意,
故应选 :A .
①如果添加∠BAD=∠CAD;能推出△ABC为等腰三角形 ,理由如下 :根据垂直的定义得出∠ADB=∠ADC=90° , 然后利用ASA判断出 △ADC≌△ADB ,根据全等三角形对应边相等得出 AB=AC ,从而得出结论△ABC是等腰三角形;
②如果添加BD=CD;能推出△ABC为等腰三角形,理由如下:根据垂直的定义得出∠ADB=∠ADC=90° , 然后利用SAS判断出 △ADC≌△ADB ,根据全等三角形对应边相等得出 AB=AC ,从而得出结论△ABC是等腰三角形;
③如果添加∠B=∠C;能推出△ABC为等腰三角形,理由如下:根据垂直的定义得出∠ADB=∠ADC=90° , 然后利用AAS判断出 △ADC≌△ADB ,根据全等三角形对应边相等得出 AB=AC ,从而得出结论△ABC是等腰三角形;从而得出答案。


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,若点
,若点![]() 的纵坐标满足
的纵坐标满足![]() , 则称点
, 则称点![]() 是点
是点![]() 的“绝对点”.
的“绝对点”.
(![]() )点
)点![]() 的“绝对点”的坐标为.
的“绝对点”的坐标为.
(![]() )点
)点![]() 是函数
是函数![]() 的图像上的一点,点
的图像上的一点,点![]() 是点
是点![]() 的“绝对点”.若点
的“绝对点”.若点![]() 与点
与点![]() 重合,求点
重合,求点![]() 的坐标.
的坐标.
(![]() )点
)点![]() 的“绝对点”
的“绝对点”![]() 是函数
是函数![]() 的图像上的一点.当
的图像上的一点.当![]() 时,求线段
时,求线段![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A(0,2),B(﹣2,0),点D是x轴上一个动点,以AD为一直角边在一侧作等腰直角三角形ADE,∠DAE=90°,若△ABD为等腰三角形时点E的坐标为___________.
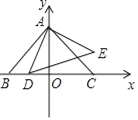
查看答案和解析>>
科目:初中数学 来源: 题型:
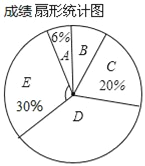
【题目】某中学为了响应国家发展足球的战略方针,激发学生对足球的兴趣,特举办全员参与的“足球比赛”,赛后,全校随机抽查部分学生,其成绩(百分制)整理分成5组,并制成如下频数分布表和扇形统计图,请根据所提供的信息解答下列问题:
成绩频数分布表
组别 | 成绩(分) | 频数 |
A | 50≤x<60 | 6 |
B | 60≤x<70 | m |
C | 70≤x<80 | 20 |
D | 80≤x<90 | 36 |
E | 90≤x<100 | n |
(1)频数分布表中的m= ,n= ;
(2)样本中位数所在成绩的级别是 ,扇形统计图中,E组所对应的扇形圆心角的度数是 ;
(3)若该校共有2000名学生,请你估计体育综合测试成绩不少于80分的大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,将点(﹣2,3)关于原点的对称点向左平移2个单位长度得到的点的坐标是( )
A.(4,﹣3)
B.(﹣4,3)
C.(0,﹣3)
D.(0,3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D为BC边的中点,F为CA的延长线上的一点,过点F 作FG⊥BC于G点,并交AB于E点.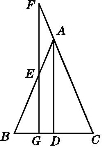
(1)求证:AD∥FG;
(2)△AFE为等腰三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com