
【题目】阅读下面材料,并回答问题:
定义:平面内与一个定点F和一条定直线l(l不经过点F)距离相等的所有点组成的图形叫抛物线.点F叫做抛物线的焦点,直线l叫做抛物线的准线.
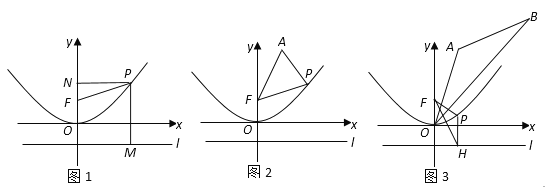
应用:(1)如图1,一条抛物线的焦点为F(0,1),准线为过点(0,-1)且平行于x轴的直线l;设点P(x,y)为抛物线上任意一点,小聪同学在应用定义求这条抛物线的解析式时作出了如下不完整的解答,请你将余下部分补充出来.
解:设点P(x,y)为抛物线上任意一点,作PM⊥l于点M,则PM=_________
作PN⊥y轴于点N,则在△PFN中,有PN=![]() ,NF=
,NF=![]() ,所以PF=__________
,所以PF=__________
∵PF=PM
∴_________=____________,
将方程两边同时平方,解得抛物线的解析式为_____________
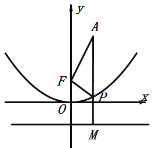
(2)如图2,在(1)的条件下,点A(1,3)是坐标平面内一点,则△FAP的周长最小值为________
(3)在(1)(2)的条件下,如图3,点B(4,4)是坐标平面内另一点,过P作PH⊥l,垂足为H,连接PF和FH,问在抛物线上是否存在点P,使得以P,F,H为顶点的三角形与△ABO相似?若存在,求出P点的坐标;若不存在,请说明理由.
【答案】(1)y+1,![]() ,y+1,
,y+1,![]() ,
,![]() ;(2)
;(2)![]() ;(3)存在,(1,
;(3)存在,(1,![]() )或(﹣1,
)或(﹣1,![]() )
)
【解析】
(1)设点P(x,y)为抛物线上任意一点,作PM⊥l于点M,根据抛物线的定义PF=PM以及两点间的距离公式得到![]() =
=![]() ,即可求解;
,即可求解;
(2)抛物线的定义知PF=PM,![]() 为定长,故当点A、P、M在同一直线上时,△FAP的周长最小,利用两点间的距离公式即可求得最小值;
为定长,故当点A、P、M在同一直线上时,△FAP的周长最小,利用两点间的距离公式即可求得最小值;
(3)根据两点间的距离公式求得AB= AO=![]() ,由抛物线的定义知PF=PH,再根据相似三角形的性质得到
,由抛物线的定义知PF=PH,再根据相似三角形的性质得到![]() ,即可求解.
,即可求解.
(1)设点P(![]() ,
,![]() )为抛物线上任意一点,作PM⊥
)为抛物线上任意一点,作PM⊥![]() 于点M,则PM=
于点M,则PM=![]() ,
,
作PN⊥y轴于点N,则在△PFN中,有PN=![]() ,NF=
,NF=![]() ,所以PF=
,所以PF=![]() ,
,
∵PF=PM,
∴![]() =
=![]() ,
,
将方程两边同时平方,解得抛物线的解析式为![]() ;
;
故答案为:y+1,![]() ,y+1,
,y+1,![]() ,
,![]() ;
;
(2)∵PF=PM,
∴点A、P、M在同一直线上时,△FAP的周长最小,如图:
![]() ,
,![]() ,
,
∴△FAP的周长最小值为:![]() ;
;
(3)存在,理由如下:
∵AB=![]() =
=![]() ,AO=
,AO=![]() =
=![]() ,OB=
,OB=![]() =4
=4![]() ,
,
∴AB=OA,
∵PF=PH,
假设存在这样的点P,使得以P,F,H为顶点的三角形与△ABO相似,
则PH与AB,FH与OB是对应边,
∴![]() ,
,
设点P(m,![]() m2),则H为(m,-1),
m2),则H为(m,-1),
则![]() ,
,
∴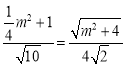 ,
,
解得:![]() ,
,
∴点P坐标(1,![]() )或(﹣1,
)或(﹣1,![]() ).
).


科目:初中数学 来源: 题型:
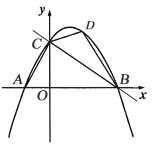
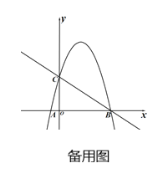
【题目】如图,在平面直角坐标系中,直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴相交于点B、C,经过点B、C的抛物线
轴相交于点B、C,经过点B、C的抛物线![]() 与
与![]() 轴的另一个交点为A.
轴的另一个交点为A.
(1)求出抛物线表达式,并求出点A坐标;
(2)已知点D在抛物线上,且横坐标为3,求出△BCD的面积;
(3)点P是直线BC上方的抛物线上一动点,过点P作PQ垂直于![]() 轴,垂足为Q.是否存在点P,使得以点A、P、Q为顶点的三角形与△BOC相似?若存在,请求出点P的坐标;若不存在,请说明理由.
轴,垂足为Q.是否存在点P,使得以点A、P、Q为顶点的三角形与△BOC相似?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
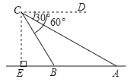
【题目】如图,一架无人机航拍过程中在![]() 处测得地面上
处测得地面上![]() ,
,![]() 两个目标点的俯角分别为
两个目标点的俯角分别为![]() 和
和![]() .若
.若![]() ,
,![]() 两个目标点之间的距离是100米,则此时无人机与目标点
两个目标点之间的距离是100米,则此时无人机与目标点![]() 之间的距离(即
之间的距离(即![]() 的长)为( )
的长)为( )
A.100米B.![]() 米C.50米D.
米C.50米D.![]() 米
米
查看答案和解析>>
科目:初中数学 来源: 题型:
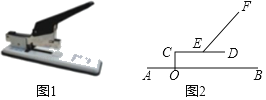
【题目】订书机是由推动器、托板、压形器、底座、定位轴等组成.如图1是一台放置在水平桌面上的大型订书机,将其侧面抽象成如图2所示的几何图形.若压形器EF的端点E固定于定位轴CD的中点处,在使用过程中,点D和点F随压形器及定位轴绕点C旋转,CO⊥AB于点O,CD=12cm连接CF,若∠FED=45°,∠FCD=30°.
(1)求FC的长;
(2)若OC=2cm求在使用过程中,当点D落在底座AB上时,请计算CD与AB的夹角及点F运动的路线之长.(结果精确到0.1cm,参考数据:sin9.6°≈0.17.π≈3.14,![]() 1.732)
1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
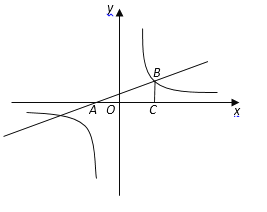
【题目】如图,平面直角坐标系中,直线![]() 与x轴交于点A,与双曲线
与x轴交于点A,与双曲线![]() 在第一象限内交于点B,BC丄x轴于点C,OC=2AO.
在第一象限内交于点B,BC丄x轴于点C,OC=2AO.
(1)求双曲线的解析式.
(2)点D为y轴上一个动点,若S△ADB=3,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,且AB=4,点C是弧AB上的一动点(不与A,B重合),过点B作⊙O的切线交AC的延长线于点D,点E是BD的中点,连接EC.
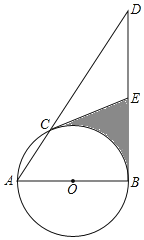
(1)若BD=8,求线段AC的长度;
(2)求证:EC是⊙O的切线;
(3)当∠D=30°时,求图中阴影部分面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() (
(![]() 是常数,
是常数,![]() )图象的对称轴是直线
)图象的对称轴是直线![]() ,其图象的一部分如图所示,下列说法中①
,其图象的一部分如图所示,下列说法中①![]() ;②
;②![]() ;③当
;③当![]() 时,
时,![]() ;④
;④![]() ;⑤
;⑤![]() .正确的结论有( )
.正确的结论有( )
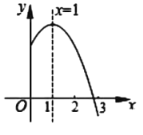
A.①②④B.②③④C.①③⑤D.①②③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
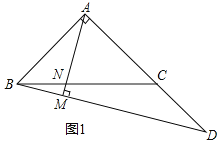
【题目】如图,在![]() 中,
中,![]() ,点D为AC延长线上一点,连接BD,过A作
,点D为AC延长线上一点,连接BD,过A作![]() ,垂足为M,交BC于点N
,垂足为M,交BC于点N
![]() 如图1,若
如图1,若![]() ,
,![]() ,求AM的长;
,求AM的长;
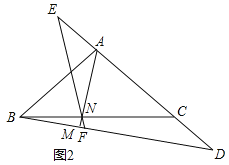
![]() 如图2,点E在CA的延长线上,且
如图2,点E在CA的延长线上,且![]() ,连接EN并延长交BD于点F,求证:
,连接EN并延长交BD于点F,求证:![]() ;
;
![]() 在
在![]() 的条件下,当
的条件下,当![]() 时,请求出
时,请求出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB,

(1)求抛物线的解析式;
(2)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值;
(3)若点E在x轴上,点P在抛物线上.是否存在以A,C,E,P为顶点且以AC为一边的平行四边形?若存在,写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com