
【题目】如图,已知直线![]() ∥
∥![]() ,且
,且![]() 和
和![]() ,
,![]() 分别交于A,B两点,
分别交于A,B两点,![]() 和
和![]() ,
,![]() 相交于C,D两点,点P在直线AB上,
相交于C,D两点,点P在直线AB上,
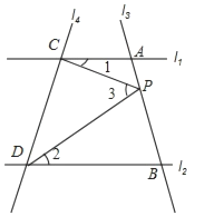
(1)当点P在A,B两点间运动时,问∠1,∠2,∠3之间的关系是否发生变化?如果不发生变化它们之间满足什么关系?并说明理由;
(2)如果点P在A,B两点外侧运动时,试探究∠ACP,∠BDP,∠CPD之间的关系,并说明理由.
【答案】(1)∠3=∠1+∠2,见解析;(2)∠CPD=∠BDP-∠ACP或∠CPD =∠ACP -∠BDP.
【解析】
(1)过点P作l1的平行线,根据平行线的性质进行解题;
(2)过点P作l1的平行线PF,由平行线的性质可得出l1∥l2∥PF,由此即可得出结论.
解:(1)如图1,过点P作PQ∥l1,
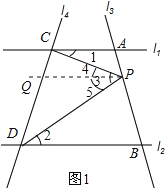
∵PQ∥l1,
∴∠1=∠4(两直线平行,内错角相等),
∵PQ∥l1,l1∥l2(已知),
∴PQ∥l2(平行于同一条直线的两直线平行),
∴∠5=∠2(两直线平行,内错角相等),
∵∠3=∠4+∠5,
∴∠3=∠1+∠2(等量代换);
(2)如图2,过P点作PF∥BD交CD于F点,
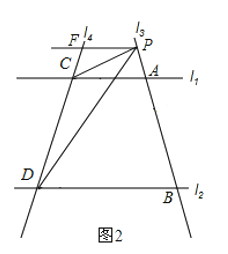
∵AC∥BD,
∴PF∥AC,
∴∠ACP=∠CPF,∠BDP=∠DPF,
∴∠CPD=∠DPF-∠CPF=∠BDP-∠ACP;
如图③,过P点作PF∥BD交CD于F点,
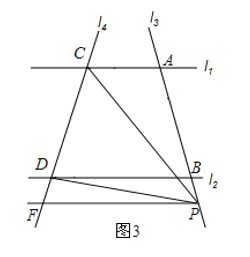
∵AC∥BD,
∴PF∥AC,
∴∠ACP=∠CPF,∠BDP=∠DPF,
∴∠CPD=∠CPF - ∠DPF =∠ACP -∠BDP;


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将坐标原点O沿x轴向左平移2个单位长度得到点A,过点A作y轴的平行线交反比例函数y=![]() 的图象于点B,AB=
的图象于点B,AB=![]() .
.
(1)求反比例函数的解析式;
(2)若P(x1,y1)、Q(x2,y2)是该反比例函数图象上的两点,且x1<x2时,y1>y2,指出点P、Q各位于哪个象限?并简要说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面推理过程:

如图,已知∠1 =∠2,∠B =∠C,可推得AB∥CD.理由如下:
∵∠1 =∠2(已知),
且∠1 =∠CGD(______________ _________),
∴∠2 =∠CGD(等量代换).
∴CE∥BF(___________________ ________).
∴∠ =∠C(__________________________).
又∵∠B =∠C(已知),
∴∠ =∠B(等量代换).
∴AB∥CD(________________________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副直角三角板如图摆放,点C在EF上,AC经过点D.已知∠A=∠EDF=90°,AB=AC.∠E=30°,∠BCE=40°,则∠CDF= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E,F分别在BC,CD上,将△ABE沿AE折叠,使点B落在AC上的点B′处,又将△CEF沿EF折叠,使点C落在EB′与AD的交点C′处.则CF:AB的值为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,∠1=∠ACB,∠2=∠3,FH⊥AB于H,求证:CD⊥AB.
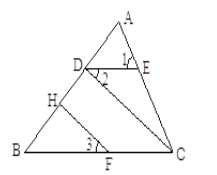
证明:∵∠1=∠ACB(已知)
∴DE∥BC( )
∴∠2= ( )
∵∠2=∠3(已知)
∴∠3=
∴CD∥FH( )
∴∠BDC=∠BHF( )
又∵FH⊥AB(已知)
∴ ( )
∵CD∥FH
∴∠BHF=∠BDC=90°( )
即CD⊥AB( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的方格地面上,标有编号A,B,C的3个小方格地面是空地,另外6个小方格地面是草坪,除此以外小方格地面完全相同.
(1)一只自由飞行的鸟,将随意地落在图中的方格地面上,问小鸟落在草坪上的概率是多少?
(2)现从3个小方格空地中任意选取2个种植草坪,则刚好选取A和B的2个小方格空地种植草坪的概率是多少(用树形图或列表法求解)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的顶点A在第一象限,点B,C的坐标为(2,1),(6,1),∠BAC=90°,AB=AC,直线AB交x轴于点P.若△ABC与△A'B'C'关于点P成中心对称,则点A'的坐标为 . 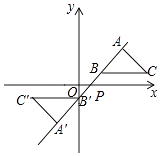
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个形状、大小完全相同的含有30°、60°的直角三角板如图①放置,PA、PB与直线MN重合,且三角板PAC、三角板PBD均可绕点P逆时针旋转.
(1)直接写出∠DPC的度数.
(2)如图②,在图①基础上,若三角板PAC的边PA从PN处开始绕点P逆时针旋转,转速为5°/秒,同时三角板PBD的边PB从PM处开始绕点P逆时针旋转,转速为1°/秒,(当PA转到与PM重合时,两三角板都停止转动),在旋转过程中,当PC与PB重合时,求旋转的时间是多少?
(3)在(2)的条件下,PC、PB、PD三条射线中,当其中一条射线平分另两条射线的夹角时,请直接写出旋转的时间.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com