练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图已知∠1与线段a，用直尺和圆规按下列步骤作图（保留作图痕迹，不写做法。）

    (1)作等∠A于∠1

    (2)在∠A的两边分别作AM=AN=a

    (3)连接MN

    【答案】（1）图见解析；（2）图见解析；（3）图见解析.

    【解析】

    （1）如图（见解析），设为，作法如下：①作射线AG；②以O为圆心，以任意长为半径画弧，交OP于点D，交OQ于点E；③以A为圆心，以OD的长为半径画弧，交AG于点B；④以点B为圆心，以DE的长为半径画弧，交前弧于点C；⑤过点C作射线AH，则就是所要作的角；

    （2）如图（见解析），以点A为圆心，以a的长为半径画弧，交射线AG于点M，交射线AH于点N，则AM、AN就是所求作的线段；

    （3）如图（见解析），连接题（2）中的点M和点N即可得.

    （1）如图，设为，作法如下：①作射线AG；②以O为圆心，以任意长为半径画弧，交OP于点D，交OQ于点E；③以A为圆心，以OD的长为半径画弧，交AG于点B；④以点B为圆心，以DE的长为半径画弧，交前弧于点C；⑤过点C作射线AH，则就是所要作的角；

    （2）以点A为圆心，以a的长为半径画弧，交射线AG于点M，交射线AH于点N，则AM、AN就是所求作的线段；

    （3）连接题（2）中的点M和点N即可得；

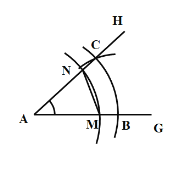
    （1）、（2）、（3）画图结果如下：

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，矩形纸片ABCD中，已知AD =8，折叠纸片使AB边与对角线AC

    重合，点B落在点F处，折痕为AE，且EF=3，则AB的长为( )

    A. 3 B. 4

    C. 5 D. 6

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，O为坐标原点，△ABO的边AB垂直与x轴，垂足为点B，反比例函数（x＞0）的图象经过AO的中点C，且与AB相交于点D，OB=4，AD=3．

    （1）求反比例函数的解析式；

    （2）求cos∠OAB的值；

    （3）求经过C、D两点的一次函数解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在矩形ABCD中，E是对角线BD上一点（不与点B、D重合），过点E作EF∥AB，且EF=AB，连接AE、BF、CF。

    （1）若DE=DC，求证：四边形CDEF是菱形；

    （2）若AB=，BC=3，当四边形ABFE周长最小时，四边形CDEF的周长为__________。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某青春党支部在精准扶贫活动中，给结对帮扶的贫困家庭赠送甲、乙两种树苗让其栽种．已知乙种树苗的价格比甲种树苗贵10元，用480元购买乙种树苗的棵数恰好与用360元购买甲种树苗的棵数相同．

    （1）求甲、乙两种树苗每棵的价格各是多少元？

    （2）在实际帮扶中，他们决定再次购买甲、乙两种树苗共50棵，此时，甲种树苗的售价比第一次购买时降低了10%，乙种树苗的售价不变，如果再次购买两种树苗的总费用不超过1500元，那么他们最多可购买多少棵乙种树苗？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC在平面直角坐标系中：

    （1）画出△ABC关于y轴对称的△DEF（其中D、E、F是A、B、C的对应点）

    （2）写出D、E、F的坐标；

    （3）求出△DEF的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，在平面直角坐标系xOy中，抛物线的图像与x轴交于点A（3，0），与y轴交于点B，顶点C在直线上，将抛物线沿射线 AC的方向平移，

    当顶点C恰好落在y轴上的点D处时，点B落在点E处．

    （1）求这个抛物线的解析式；

    （2）求平移过程中线段BC所扫过的面积；

    （3）已知点F在x轴上，点G在坐标平面内，且以点 C、E、F、G 为顶点的四边形是矩形，求点F的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系xoy中，O为原点，ABCD的边AB在x轴上，点D在y轴上，点A的坐标为（﹣2，0），AB=6，∠BAD=60°，点E是BC边上一点，CE=3EB，⊙P过A、O、D三点，抛物线y=ax2+bx+c过点A、B、D三点．

    （1）求抛物线的解析式；

    （2）求证：DE是⊙P的切线；

    （3）若将△CDE绕点D顺时针旋转90°，点E的对应点E′会落在抛物线y=ax2+bx+c上吗？请说明理由；

    （4）若点M为此抛物线的顶点，平面上是否存在点N，使得以点B、D、M、N为顶点的四边形为平行四边形？若存在，请直接写出点N的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知AB是⊙O的弦，OB=2，∠B=30°，C是弦AB上任意一点（不与点A、B重合），连接CO并延长CO交⊙O于点D，连接AD．

    （1）AB=_____；

    （2）当∠D=20°时，求∠BOD的度数．

    （3）若△ACD与△BCO相似，求AC的长．

    查看答案和解析>>

    同步练习册答案