
【题目】如图,在平面直角坐标系xOy中,菱形ABCD的顶点A的坐标为(2,0),点B的坐标为(0,1),点C在第一象限,对角线BD与x轴平行.直线y=x+4与x轴、y轴分别交于点E,F.将菱形ABCD沿x轴向左平移k个单位,当点C落在△EOF的内部时(不包括三角形的边),k的值可能是( )
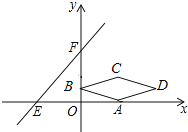
A.2 B.3 C.4 D.5
【答案】B
【解析】
试题分析:连接AC,BD,交于点Q,过C作y轴垂线,交y轴于点M,交直线EF于点N,如图所示,由菱形ABCD,根据A与B的坐标确定出C坐标,进而求出CM与CN的值,确定出当点C落在△EOF的内部时k的范围,即可求出k的可能值.
解:连接AC,BD,交于点Q,过C作y轴垂线,交y轴于点M,交直线EF于点N,如图所示,
∵菱形ABCD的顶点A的坐标为(2,0),点B的坐标为(0,1),点C在第一象限,对角线BD与x轴平行,
∴CQ=AQ=1,CM=2,即AC=2AQ=2,
∴C(2,2),
当C与M重合时,k=CM=2;当C与N重合时,把y=2代入y=x+4中得:x=﹣2,即k=CN=CM+MN=4,
∴当点C落在△EOF的内部时(不包括三角形的边),k的范围为2<k<4,
则k的值可能是3,
故选B


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC是直角三角形,∠ACB=90°

(1)利用尺规作∠ABC 的平分线,交AC 于点O,再以O 为圆心,OC 的长为半径作⊙O(保留作图痕迹,不写作法);
(2)在你所作的图中,①判断AB 与⊙O 的位置关系,并证明你的结论;②若AC=12,tan∠OBC=![]() ,求⊙O 的半径。
,求⊙O 的半径。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)先化简,再求值:2![]() +(
+(![]() +
+![]() )(
)( ![]() -2
-2![]() )-(
)-(![]() -
-![]() ,其中
,其中![]() =-3,
=-3, ![]() =
=![]() .
.
(2)已知ab=-3,a+b=2.求下列各式的值:
①a2+b2;
②a3b+2a2b2 +ab3;
③a-b.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】写出下列命题的条件与结论.
(1)两条直线平行,同位角相等;
(2)同角或等角的补角相等;
(3)两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一种大米的质量标识为“(50±0.5)千克”,则下列各袋大米中质量不合格的是( )
A. 50.0千克 B. 50.3千克 C. 49.7千克 D. 49.1千克
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】类比、转化、从特殊到一般等思想方法,在数学学习和研究中经常用到,如下是一个案例,请补充完整.
原题:如图1,在ABCD中,点E是BC边上的中点,点F是线段AE上一点,BF的延长线交射线CD于点G,若![]() =3,求
=3,求![]() 的值.
的值.
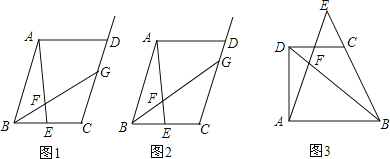
(1)尝试探究
在图1中,过点E作EH∥AB交BG于点H,则AB和EH的数量关系是 ,CG和EH的数量关系是 ,![]() 的值是
的值是
(2)类比延伸
如图2,在原题的条件下,若![]() =m(m≠0),则
=m(m≠0),则![]() 的值是 (用含m的代数式表示),试写出解答过程.
的值是 (用含m的代数式表示),试写出解答过程.
(3)拓展迁移
如图3,梯形ABCD中,DC∥AB,点E是BC延长线上一点,AE和BD相交于点F,若![]() =a,
=a,![]() =b(a>0,b>0),则
=b(a>0,b>0),则![]() 的值是 (用含a,b的代数式表示).
的值是 (用含a,b的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
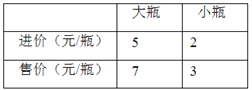
【题目】已知某品牌的饮料有大瓶和小瓶装之分,某超市花了3800元购进一批该品牌的饮料共1000瓶,其中,大瓶和小瓶饮料的进价及售价如表所示.
(1)问:该超市购进大瓶和小瓶饮料各多少瓶?
(2)当大瓶饮料售出了200瓶,小瓶饮料售出了100瓶后,商家决定将剩下的小瓶饮料的售价降低0.5元销售,并把其中一定数量的小瓶饮料作为赠品,在顾客一次购买大瓶饮料时,每满2瓶就送1瓶饮料,送完即止.请问:超市要使这批饮料售完后获得的利润不低于1250元,那么小瓶饮料作为赠品最多只能送出多少瓶?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题是假命题的是( )
A. 四个角相等的四边形是矩形
B. 对角线相等的平行四边形是矩形
C. 对角线垂直的四边形是菱形
D. 对角线垂直的平行四边形是菱形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com