
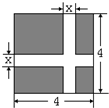
 如图,图中的阴影部分的面积是________.
如图,图中的阴影部分的面积是________. 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案科目:初中数学 来源: 题型:
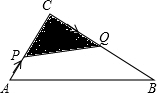 已知:如图,△ABC中,∠C=90°,AC=3厘米,CB=4厘米.两个动点P、Q分别从A、C两点同时按顺时针方向沿△ABC的边运动.当点Q运动到点A时,P、Q两点运动即停止.点P、Q的运动速度分别为1厘米/秒、2厘米/秒,设点P运动时间为t(秒).
已知:如图,△ABC中,∠C=90°,AC=3厘米,CB=4厘米.两个动点P、Q分别从A、C两点同时按顺时针方向沿△ABC的边运动.当点Q运动到点A时,P、Q两点运动即停止.点P、Q的运动速度分别为1厘米/秒、2厘米/秒,设点P运动时间为t(秒).查看答案和解析>>
科目:初中数学 来源: 题型:
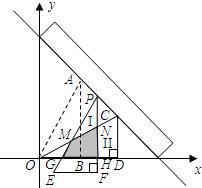 从上方紧靠两纸板放置,让纸板Ⅰ沿直尺边缘平行移动.当纸板Ⅰ移动至△PEF处时,设PE,PF与OC分别交于点M,N,与x轴分别交于点G,H.
从上方紧靠两纸板放置,让纸板Ⅰ沿直尺边缘平行移动.当纸板Ⅰ移动至△PEF处时,设PE,PF与OC分别交于点M,N,与x轴分别交于点G,H.查看答案和解析>>
科目:初中数学 来源: 题型:
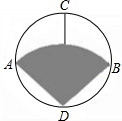 某种商品的商标图案如图(图中的阴影部分),已知⊙O的直径AB⊥CD,且AB=8cm,弧AB是以D为圆心,DA为半径的弧,则商标图案的面积为
某种商品的商标图案如图(图中的阴影部分),已知⊙O的直径AB⊥CD,且AB=8cm,弧AB是以D为圆心,DA为半径的弧,则商标图案的面积为查看答案和解析>>
科目:初中数学 来源:第26章《二次函数》中考题集(36):26.3 实际问题与二次函数(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com