
����Ŀ���ڡ�ABC�У���ABΪб�ߣ���ֱ�ǡ�ABD��ʹ��D���ڡ�ABC�ڣ���ADB=90�㣮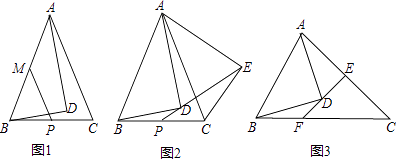
��1����ͼ1����AB=AC����DBA=60�㣬AD=7 ![]() ����P��M�ֱ�ΪBC��AB�ߵ��е㣬����PM�����߶�PM�ij���
����P��M�ֱ�ΪBC��AB�ߵ��е㣬����PM�����߶�PM�ij���
��2����ͼ2����AB=AC���ѡ�ABD�Ƶ�A��ʱ����תһ���Ƕȣ��õ���ACE������ED���ӳ���BC�ڵ�P����֤��BP=CP��
��3����ͼ3����AD=BD������D��ֱ�߽�AC�ڵ�E����BC�ڵ�F��EF��AC����AE=EC����ֱ��д���߶�BF��FC��AD֮��Ĺ�ϵ������Ҫ֤������
���𰸡�
��1��
�⣺��ͼ1�У�

�ߡ�ADB=90�㣬��DBA=60�㣬AD=7 ![]() ��
��
���BAD=30�㣬
��AB=2BD����BD=a����AB=2a��
��AB2=BD2+AD2��
�ࣨ2a��2=a2+��7 ![]() ��2��
��2��
��a=7��
��AB=AC=14��
��AM=MB��PB=PC��
��PM= ![]() AC=7
AC=7
��2��
֤������ͼ2�У���ED�Ͻ�ȡEQ=DP������CQ��

��AD=AE��
���1=��2��
�ߡ�ADB=��AEC=90�㣬
���1+��3=90�㣬��2+��4=90�㣬
���3=��4��
��BD=EC��
���EQC�ա�DPB��
��CQ=BP����QCE=��DBP��
�ߡ�CQP=��3+��QCE����CPQ=��4+��DBP��
���CQP=��CPQ��
��CQ=PC��
��PB=PC��
��3��
�⣺���ۣ�2AD2=FB2+CF2��
���ɣ���ͼ3�У�����AF��BD��N������CD�ӳ���H��

��EA=EC��EF��AC��
��DA=DC��
�ߡ�ADB=90�㣬DA=DB��
��DA=DC=DB�����DBA=��DAB=45�㣬AB= ![]() AD��
AD��
���DAC=��DCA����DBC=��DCB��
�ߡ�ADH=��DAC+��ACD����BDH����DBC+��DCB��
���ADB=2��ACD+2��DCB=90�㣬
���ACF=45�㣬
��FA=FC��
���FAC=��FCA=45�㣬
���AFC=90��
�ߡ�AND=��BNF����ADN=��BFN=90�㣬
���AND�ס�BNF��
�� ![]() ��
��
�� ![]() ���ߡ�ANB=��DNF��
���ߡ�ANB=��DNF��
���ANB�ס�DNF��
���DFN=��ABD=45�㣬
��FE��AC��AE=EC��
��FA=FC����AFE=��CFE=45�㣬
���AFC=��AFB=90�㣬
��AB2=BF2+AF2��
��2AD2=BF2+CF2
����������1������ֱ��������30�Ƚ��������AB���ٸ�����������λ�߶����������PM����2����ͼ2�У���ED�Ͻ�ȡEQ=DP������CQ������֤����EQC�ա�DPB���Ƴ�QC=PB����֤��QC=PC���ɽ�����⣮��3�����ۣ�2AD2=FB2+CF2 �� ��ͼ3�У�����AF��BD��N���ɡ�AND�ס�BNF���Ƴ� ![]() ���Ƴ�
���Ƴ� ![]() ���֡�ANB=��DNF���Ƴ���ANB�ס�DNF���ӡ�DFN=��ABD=45�㣬��RtABF�����ù��ɶ�������֤����
���֡�ANB=��DNF���Ƴ���ANB�ס�DNF���ӡ�DFN=��ABD=45�㣬��RtABF�����ù��ɶ�������֤����
�����㾫����������Ŀ����֪���������ù��ɶ����ĸ������������λ�߶��������֪ʶ���Եõ�����Ĵ𰸣���Ҫ����ֱ����������ֱ�DZ�a��b��ƽ���͵���б��c��ƽ��,��;a2+b2=c2�����������������е���߶ν��������ε���λ������������λ�߶����������ε���λ��ƽ���������εĵ����ߣ��ҵ��ڵ����ߵ�һ�룮


 һ���㶨ϵ�д�
һ���㶨ϵ�д� ��У��ҵ��ϵ�д�
��У��ҵ��ϵ�д� ���ɶ���ܲ��¿�ֱͨ��Уϵ�д�
���ɶ���ܲ��¿�ֱͨ��Уϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�����κ���y=��x2+bx+c��ͼ����㣨��1����8������0����3����
��1����˶��κ����ı���ʽ�������䷽�����仯Ϊy=a��x��h��2+k����ʽ��
��2������㷨�����˺���ͼ���ʾ��ͼ�� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
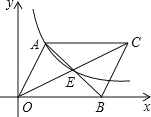
����Ŀ����ͼ��ƽ���ı���AOBC�����Խ��߽��ڵ�E��˫����y=![]() ��k��0������A��E������ ��ƽ���ı���AOBC�����Ϊ30����k=__________��
��k��0������A��E������ ��ƽ���ı���AOBC�����Ϊ30����k=__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ս�п���������ѧ���Ǹо������ص�˯�߲��㣬������������ͬѧ�ǵ�˯��ʱ�䣬�Ƴ�����ͼ����ͳ��ͼ�� 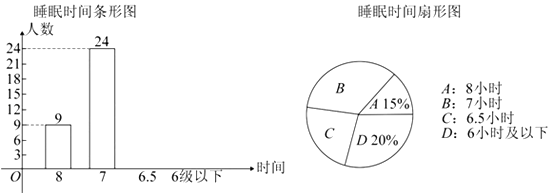
���������ͼ�ν���������⣺
��1��������ͳ��ͼ����������������ͳ��ͼ��B���������ε�Բ�Ľ��� ��
��2��˯��ʱ�����λ���� ��
��3�������˯��ʱ�����7Сʱ��Ϊ����˯�߲��㣬�����ȫУ2800������ͬѧ��˯�����ز����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������Ӳֽ�������������ӣ�ÿ��������3�����β����2���������ε�����ɡ�Ӳֽ������ͼ���ַ�ʽ�ü����ü���߽��ϲ������ã�
A��������6�����棻 B��������4�������5�����档

����19��Ӳֽ�壬�ü�ʱ![]() ����A������������B������
����A������������B������
��1����![]() �Ĵ���ʽ�ֱ��ʾ�ü����IJ���͵���ĸ�����
�Ĵ���ʽ�ֱ��ʾ�ü����IJ���͵���ĸ�����
��2�����ü����IJ���͵���ǡ��ȫ�����꣬���������ٸ����ӣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=x2��3x+m��mΪ��������ͼ����x���һ������Ϊ��1��0���������x��һԪ���η���x2��3x+m=0����ʵ�����ǣ� ��
A.x1=1��x2=��1
B.x1=1��x2=2
C.x1=1��x2=0
D.x1=1��x2=3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�ı߳�Ϊ4����P��Q�ֱ���CD��AD���е㣬����E�ӵ�A���B�˶�������Bʱֹͣ�˶���ͬʱ������F�ӵ�P��������P��D��Q�˶�����E��F���˶��ٶ���ͬ�����E���˶�·��Ϊx����AEF�����Ϊy���ܴ��¿̻�y��x�ĺ�����ϵ��ͼ���ǣ� ��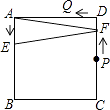
A.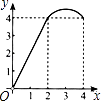
B.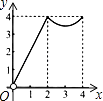
C.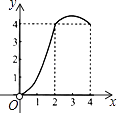
D.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ��ʾ��ֱ������ϵ�У�����������⣺ 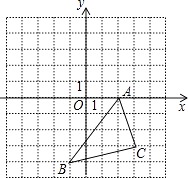
��1���ֱ�д��A��B��������ꣻ
��2������ABC�Ƶ�A˳ʱ����ת90�㣬������ת��ġ�AB1C1��
��3������߶�B1A����ֱ��l�ĺ�������ʽ����д����ֱ��l�ϴ�B1��A���Ա���x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������жϣ��ٵ���ʽ5��103x2��ϵ����5���ڵ�x�ֱ�ȡ2�ͣ�2ʱ������ʽx3��2x��ֵ��Ϊ�෴�� ���۶���ʽ��3a2b��7a2b2��2ab��1�Ĵ�����9����������ʽ3x2ym��2��xn-1y�ĺ���Ȼ��һ������ʽ����m��n��ֵ�ֱ��ǣ�1��3���ݼ�����������ˣ����������ĸ���Ϊ����ʱ����Ϊ�����������ж���ȷ����________________ .(����ȷ�𰸵�������ں�����)
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com