
【题目】在平面直角坐标系中,点![]() ,
,![]() ,点C为x轴正半轴上一动点,过点A作
,点C为x轴正半轴上一动点,过点A作![]() 交y轴于点E.
交y轴于点E.

![]() 如图
如图![]() ,若点C的坐标为
,若点C的坐标为![]() ,试求点E的坐标;
,试求点E的坐标;
![]() 如图
如图![]() ,若点C在x轴正半轴上运动,且
,若点C在x轴正半轴上运动,且![]() , 其它条件不变,连接DO,求证:OD平分
, 其它条件不变,连接DO,求证:OD平分![]()
![]() 若点C在x轴正半轴上运动,当
若点C在x轴正半轴上运动,当![]() 时,求
时,求![]() 的度数.
的度数.
【答案】(1)点E的坐标为(0,2);(2)详见解析;(3)∠OCB=60°.
【解析】
(1)先根据AAS判定△AOE≌△BOC,得出OE=OC,再根据点C的坐标为(2,0),得到OC=2=OE,进而得到点E的坐标;
(2)先过点O作OM⊥AD于点M,作ON⊥BC于点N,根据△AOE≌△BOC,得到S△AOE=S△BOC,且AE=BC,再根据OM⊥AE,ON⊥BC,得出OM=ON,进而得到OD平分∠ADC;
(3)在DA上截取DP=DC,连接OP,根据SAS判定△OPD≌△OCD,再根据三角形外角性质以及三角形内角和定理,求得∠PAO=30°,进而得到∠OCB=60°.
(1)如图①,∵AD⊥BC,BO⊥AO,
∴∠AOE=∠BDE,
又∵∠AEO=∠BED,
∴∠OAE=∠OBC,
∵A(-3,0),B(0,3),
∴OA=OB=3,
∴△AOE≌△BOC,
∴OE=OC,
又∵点C的坐标为(2,0),
∴OC=2=OE,
∴点E的坐标为(0,2);
(2)如图②,过点O作OM⊥AD于点M,作ON⊥BC于点N,
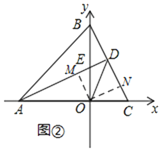
∵△AOE≌△BOC,
∴S△AOE=S△BOC,且AE=BC,
∵OM⊥AE,ON⊥BC,
∴OM=ON,
∴OD平分∠ADC;
(3)如所示,在DA上截取DP=DC,连接OP,
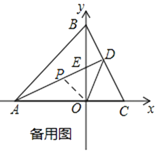
∵∠PDO=∠CDO,OD=OD,
∴△OPD≌△OCD,
∴OC=OP,∠OPD=∠OCD,
∵AD-CD=OC,
∴AD-DP=OP,即AP=OP,
∴∠PAO=∠POA,
∴∠OPD=∠PAO+∠POA=2∠PAO=∠OCB,
又∵∠PAO+∠OCD=90°,
∴3∠PAO=90°,
∴∠PAO=30°,
∴∠OCB=60°.


科目:初中数学 来源: 题型:
【题目】已知:p为实数.
p | k | q |
… | … | … |
3 | 16×3+26 | 2×2×6 |
4 | 16×4+26 | 2×3×7 |
5 | 16×5+26 | 2×4×8 |
6 | 16×6+26 | 2×5×9 |
7 | 16×7+26 | 2×6×10 |
… | … | … |
根据上表中的规律,回答下列问题:
(1)当p为何值时,k=38?
(2)当p为何值时,k与q的值相等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() ,OE平分
,OE平分![]() ,点A、B、C分别是射线OM、OE、ON上的动点
,点A、B、C分别是射线OM、OE、ON上的动点![]() 、B、C不与点O重合
、B、C不与点O重合![]() ,连接AC交射线OE于点
,连接AC交射线OE于点![]() 设
设![]() .
.

![]() 如图1,若
如图1,若![]() ,则
,则
![]() 的度数是______;
的度数是______;
![]() 当
当![]() 时,
时,![]() ______;当
______;当![]() 时,
时,![]() ______.
______.
![]() 如图2,若
如图2,若![]() ,则是否存在这样的x的值,使得
,则是否存在这样的x的值,使得![]() 中有两个相等的角?若存在,求出x的值;若不存在,说明理由.
中有两个相等的角?若存在,求出x的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,有以下四个结论:①HE=HF;②EC平分∠DCH;③线段BF的取值范围为3≤BF≤4;④当点H与点A重合时,EF=2![]() .以上结论中,你认为正确的有( )个.
.以上结论中,你认为正确的有( )个.

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数y=-![]() 的图象的两个分支分布在第_________象限,在每个象限内,y随x的增大而_________,函数y=
的图象的两个分支分布在第_________象限,在每个象限内,y随x的增大而_________,函数y=![]() 的图象的两个分支分布在第_________象限,在每一个象限内,y随x的减小而_________.
的图象的两个分支分布在第_________象限,在每一个象限内,y随x的减小而_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
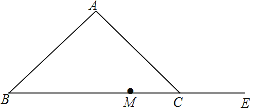
【题目】如图,在△ABC中,AB=AC.
(1)尺规作图:作∠ABC的平分线,交AC于点D(保留作图痕迹,不写作法);
(2)E是底边BC的延长线上一点,M是BE的中点,连接DE,DM,若CE=CD,求证:DM⊥BE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场今年2月份的营业额为400万元,3月份的营业额比2月份增加10%,5月份的营业额达到633.6万元.求3月份到5月份营业额的月平均增长率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形ABCD中,AB=8,AD=10,点E为BC上一点,将△ABE沿AE折叠,使点B落在长方形内点F处,且DF=6.

(1)试说明:△ADF是直角三角形;
(2)求BE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com