
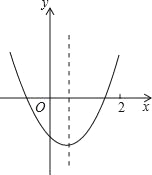
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论(1)4a+2b+c>0;(2)方程ax2+bx+c=0两根之和小于零;(3)y随x的增大而增大;(4)一次函数y=x+bc的图象一定不过第二象限.其中正确的个数是( )
A. 4 个B. 3个C. 2个D. 1个
【答案】D
【解析】
根据函数的图象可知x=2时,函数值的正负性,即可对(1)作出判断;根据函数图象的开口方向得出a的符号,根据对称轴在y轴右侧可得出b的符号,根据图象与y轴的交点可得出c的符号,根据一元二次方程根与系数的关系即可对(2)作出判断;二次函数的增减性需要找到其对称轴才知具体情况,故(3)错误;根据b、c的符号即可得出一次函数y=x+bc所经过的象限进而对(4)作出判断.
解:∵当x=2时,y=4a+2b+c,由图象可知当x=2时对应的点在x轴的上方,即4a+2b+c>0;故(1)正确;
由二次函数y=ax2+bx+c(a≠0)的图象可知:图象开口向上,a>0,对称轴在y轴右侧,![]() >0,所以b<0,图象与y轴交在负半轴,c<0,所以一元二次方程ax2+bx+c =0的两根之和为
>0,所以b<0,图象与y轴交在负半轴,c<0,所以一元二次方程ax2+bx+c =0的两根之和为![]() >0,故(2)错误;
>0,故(2)错误;
因为函数的增减性需要找到其对称轴才知具体情况,不能在整个自变量取值范围内说y随x的增大而增大,故(3)错误;
因为c<0,b<0,
所以bc>0,
所以一次函数y=x+bc的图象一定经过第二象限,故(4)错误.
所以正确的个数是1个.
故选:D.


科目:初中数学 来源: 题型:
【题目】(1)问题发现
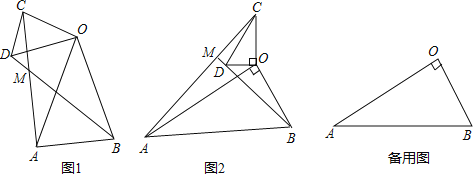
如图1,在△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=40°,连接AC,BD交于点M.填空:
①![]() 的值为 ;
的值为 ;
②∠AMB的度数为 .
(2)类比探究
如图2,在△OAB和△OCD中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,连接AC交BD的延长线于点M.请判断![]() 的值及∠AMB的度数,并说明理由;
的值及∠AMB的度数,并说明理由;
(3)拓展延伸
在(2)的条件下,将△OCD绕点O在平面内旋转,AC,BD所在直线交于点M,若OD=1,OB=![]() ,请直接写出当点C与点M重合时AC的长.
,请直接写出当点C与点M重合时AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在大楼AB正前方有一斜坡CD,坡角∠DCE=30°,楼高AB=60米,在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的D处测得楼顶B的仰角为45°,其中点A,C,E在同一直线上.
(1)求坡底C点到大楼距离AC的值;
(2)求斜坡CD的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
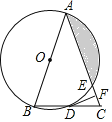
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC、AC交于点D、E,过点D作DF⊥AC于点F.
(1)若⊙O的半径为3,∠CDF=15°,求阴影部分的面积;
(2)求证:DF是⊙O的切线;
(3)求证:∠EDF=∠DAC.
查看答案和解析>>
科目:初中数学 来源: 题型:
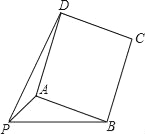
【题目】已知:PA=![]() ,PB=4,以AB为一边作正方形ABCD,使P、D两点落在直线AB的两侧.
,PB=4,以AB为一边作正方形ABCD,使P、D两点落在直线AB的两侧.
(1)如图,当∠APB=45°时,求AB及PD的长;
(2)当∠APB变化,且其它条件不变时,求PD的最大值,及相应∠APB的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,抛物线y=ax2+bx+2与x轴的交点是A(3,0)、B(6,0),与y轴的交点是C.

(1)求抛物线的函数表达式;
(2)设P(x,y)(0<x<6)是抛物线上的动点,过点P作PQ∥y轴交直线BC于点Q.
①当x取何值时,线段PQ的长度取得最大值,其最大值是多少?
②是否存在这样的点P,使△OAQ为直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,∠B的角平分线BE与AD交于点E,∠BED的角平分线EF与DC交于点F,若AB=9,DF=2FC,则BC=____.(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
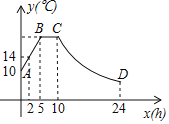
【题目】某蔬菜生产基地的气温较低时,用装有恒温系统的大棚栽培一种新品种蔬菜.如图是试验阶段的某天恒温系统从开启到关闭后,大棚内的温度y (℃)与时间x(h)之间的函数关系,其中线段AB、BC表示恒温系统开启阶段,双曲线的一部分CD表示恒温系统关闭阶段.
请根据图中信息解答下列问题:
(1)求这天的温度y与时间x(0≤x≤24)的函数关系式;
(2)求恒温系统设定的恒定温度;
(3)若大棚内的温度低于10℃时,蔬菜会受到伤害.问这天内,恒温系统最多可以关闭多少小时,才能使蔬菜避免受到伤害?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com