
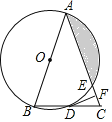
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC、AC交于点D、E,过点D作DF⊥AC于点F.
(1)若⊙O的半径为3,∠CDF=15°,求阴影部分的面积;
(2)求证:DF是⊙O的切线;
(3)求证:∠EDF=∠DAC.
【答案】(1)阴影部分的面积为3π﹣![]() ;(2)证明见解析;(3)证明见解析.
;(2)证明见解析;(3)证明见解析.
【解析】(1)连接OE,过O作OM⊥AC于M,求出AE、OM的长和∠AOE的度数,分别求出△AOE和扇形AOE的面积,即可求出答案;
(2)连接OD,求出OD⊥DF,根据切线的判定求出即可;
(3)连接BE,求出∠FDC=∠EBC,∠FDC=∠EDF,即可求出答案.
详(1)解: 连接OE,过O作OM⊥AC于M,则∠AMO=90°,
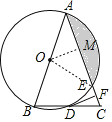
∵DF⊥AC,
∴∠DFC=90°,
∵∠FDC=15°,
∴∠C=180°-90°-15°=75°,
∵AB=AC,
∴∠ABC=∠C=75°,
∴∠BAC=180°-∠ABC∠C=30°,
∴OM=![]() OA=
OA=![]() ×3=
×3=![]() ,AM=
,AM=![]() OM=
OM=![]() ,
,
∵OA=OE,OM⊥AC,
∴AE=2AM=3![]() ,
,
∴∠BAC=∠AEO=30°,
∴∠AOE=180°-30°-30°=120°,
∴阴影部分的面积S=S扇形AOE-S△AOE=![]() ;
;
(2)证明:连接OD,

∵AB=AC,OB=OD,
∴∠ABC=∠C,∠ABC=∠ODB,
∴∠ODB=∠C,
∴AC∥OD,
∵DF⊥AC,
∴DF⊥OD,
∵OD过O,
∴DF是⊙O的切线;
(3)证明:连接BE,
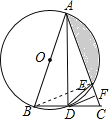
∵AB为⊙O的直径,
∴∠AEB=90°,
∴BE⊥AC,
∵DF⊥AC,
∴BE∥DF,
∴∠FDC=∠EBC,
∵∠EBC=∠DAC,
∴∠FDC=∠DAC,
∵A、B、D、E四点共圆,
∴∠DEF=∠ABC,
∵∠ABC=∠C,
∴∠DEC=∠C,
∵DF⊥AC,
∴∠EDF=∠FDC,
∴∠EDF=∠DAC.


科目:初中数学 来源: 题型:
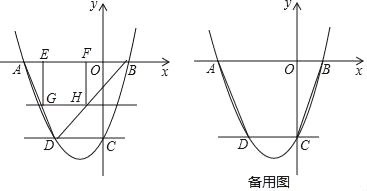
【题目】如图,已知抛物线y=ax2+bx﹣3与x轴交于点A(﹣3,0)和点B(1,0),交y轴于点C,过点C作CD∥x轴,交抛物线于点D.
(1)求抛物线的解析式;
(2)若直线y=m(﹣3<m<0)与线段AD、BD分别交于G、H两点,过G点作EG⊥x轴于点E,过点H作HF⊥x轴于点F,求矩形GEFH的最大面积;
(3)若直线y=kx+1将四边形ABCD分成左、右两个部分,面积分别为S1,S2,且S1:S2=4:5,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4,…均为等边三角形,若OA2=4,则△AnBnAn+1的边长为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
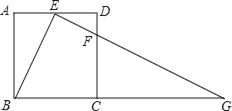
【题目】如图,在正方形ABCD中,E、F分别是边AD、CD上的点,AE=ED,DF:DC=1:4,连接EF并延长交BC的延长线于点G.
(1)求证:△ABE∽△DEF;
(2)若正方形的边长为10,求BG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
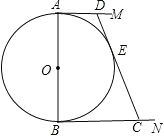
【题目】如图,⊙O的直径是AB=12cm,AM、BN是它的两条切线,DE与⊙O相切于点E,并与AM、BN分别相交于D、C两点,设AD=x,BC=y,则y与x的函数解析式为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,阳光下,小亮的身高如图中线段AB所示,他在地面上的影子如图中线段BC所示,线段DE表示旗杆的高,线段FG表示一堵高墙.
(1)请你在图中画出旗杆在同一时刻阳光照射下形成的影子,并用线段表示;
(2)如果小亮的身高AB=1.6m,他的影子BC=2.4m,旗杆的高DE=15m,旗杆与高墙的距离EG=16m,请求出旗杆的影子落在墙上的长度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com