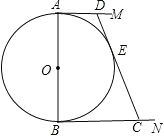
【题目】如图，⊙O的直径是AB=12cm,AM、BN是它的两条切线，DE与⊙O相切于点E，并与AM、BN分别相交于D、C两点，设AD=x,BC=y，则y与x的函数解析式为______.
轻巧夺冠周测月考直通中考系列答案科目：初中数学 来源： 题型：
【题目】如图，抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=1，与x轴的一个交点坐标为（﹣1，0），其部分图象如图所示，下列结论：①b2＞4ac；②方程ax2+bx+c=0的两个根是x1=﹣1，x2=3；③当y＞0时，x的取值范围是﹣1＜x≤3；④当x＞0时，y随x增大而增大．⑤a＞-
c上述五个结论中正确的有_________（填序号）
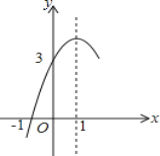
查看答案和解析>>
科目：初中数学 来源： 题型：
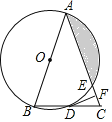
【题目】如图，在△ABC中，AB=AC，以AB为直径的⊙O分别与BC、AC交于点D、E，过点D作DF⊥AC于点F．
（1）若⊙O的半径为3，∠CDF=15°，求阴影部分的面积；
（2）求证：DF是⊙O的切线；
（3）求证：∠EDF=∠DAC．
查看答案和解析>>
科目：初中数学 来源： 题型：
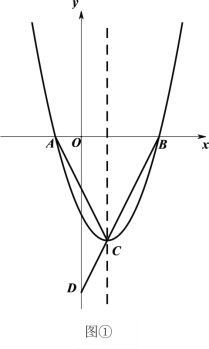
【题目】如图①，二次函数
的图像与
轴交于
、
两点（点在的左侧），顶点为
，连接
并延长交
轴于点
，若
.
（1）求二次函数的表达式；
（2）在轴上方有一点
，
，且
，连接
并延长交抛物线于点
，求点的坐标；
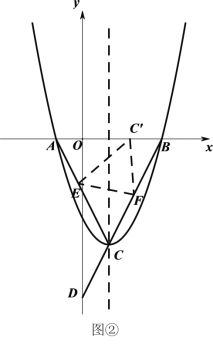
（3）如图②，折叠△
，使点落在线段
上的点
处，折痕为
．若△
有一条边与轴垂直，直接写出此时点的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某校随机抽取九年级部分同学接受一次内容为“最适合自己的考前减压方式”的调查活动，学校收集整理数据后，将减压方式分为五类，并绘制了图1、图2两个不完整的统计图，请根据图中的信息解答下列问题：
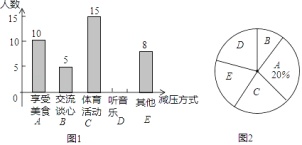
九年级接受调查的同学共有多少名，并补全条形统计图；
九年级共有500名学生，请你估计该校九年级听音乐减压的学生有多少名；
若喜欢“交流谈心”的5名同学中有三名男生和两名女生，心理老师想从5名同学中任选两名同学进行交流，请用画树状图或列表的方法求同时选出的两名同学都是女生的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
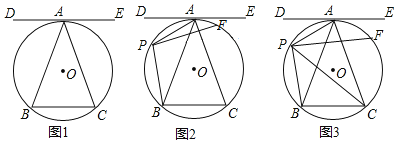
【题目】.如图，⊙O是△ABC的外接圆，直线DE是⊙O的切线，点A为切点，DE∥BC；
（1）如图1.求证：AB=AC；
（2）如图2.点P是弧AB上一动点，连接PA、PB，作PF⊥PB,垂足为点P,PF交⊙O于点F, 求证：∠BAC=2∠APF；
（3）如图3.在（2）的条件下，连接PC，PA=
，PB=
，PC=
，求线段PF的长.
查看答案和解析>>
科目：初中数学 来源： 题型：
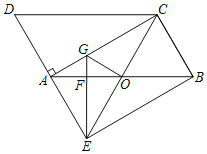
【题目】如图，在平行四边形ABCD中，
，延长DA于点E，使得
，连接BE．
求证：四边形AEBC是矩形；
过点E作AB的垂线分别交AB，AC于点F，G，连接CE交AB于点O，连接OG，若
，
，求
的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
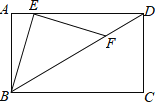
【题目】在矩形ABCD中，
，
，点E在射线DA上，连接BE，将线段BE绕点E旋转
后，点B恰好落在射线DB上
此时点B的对应点为点
，则线段DF的长为______．
查看答案和解析>>
科目：初中数学 来源： 题型：
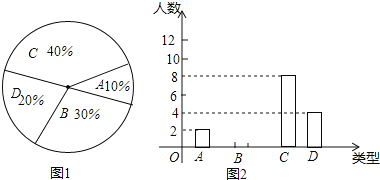
【题目】某校要求200名学生进行社会调查，每人必须完成
份报告，调查结束后随机抽查了20名学生每人完成报告的份数，并分为四类，A：3份；B：4份；C：5份；D：6份，将各类的人数绘制成扇形图
如图
和尚未完整的条形图如图
，回答下列问题：
请将条形统计图2补充完整；
写出这20名学生每天完成报告份数的众数______份和中位数______份；
在求出20名学生每人完成报告份数的平均数时，小明是这样分析的：
第一步：求平均数的公式是
；
第二步：在该问题中，
，
，
，
，
；
第三步：
(份)；
小明的分析对不对？如果对，请说明理由，如果不对，请求出正确结果．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
