
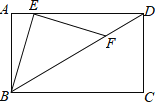
【题目】在矩形ABCD中,![]() ,
,![]() ,点E在射线DA上,连接BE,将线段BE绕点E旋转
,点E在射线DA上,连接BE,将线段BE绕点E旋转![]() 后,点B恰好落在射线DB上
后,点B恰好落在射线DB上![]() 此时点B的对应点为点
此时点B的对应点为点![]() ,则线段DF的长为______.
,则线段DF的长为______.
【答案】![]() 或105
或105
【解析】
解直角三角形得到AD=12,过F作FH⊥AD于H,设DH=4x,FH=3x,根据勾股定理得到DF=5x,根据余角的性质得到∠ABE=∠HEF,根据全等三角形的性质得到AE=HF=3x,EH=AB=9,分情况讨论列方程即可得到结论.
如图1,∵四边形ABCD是矩形,
∴∠A=90°,
∵AB=9,tan∠ADB=![]() ,
,
∴AD=12,
过F作FH⊥AD于H,
∵tan∠ADB=![]() ,
,
∴设DH=4x,FH=3x,
∴DF=5x,
∵∠BEF=90°,
∴∠ABE+∠AEB=∠AEB+∠HEF=90°,
∴∠ABE=∠HEF,
在△ABE与△HEF中,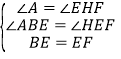 ,
,
∴△ABE≌△HEF(AAS),
∴AE=HF=3x,EH=AB=9,
∴AE+DH=AD﹣EH=3x+4x=12﹣9=3,
∴x=![]() ,
,
∴DF=5x=![]() ;
;
如图2,∵四边形ABCD是矩形,
∴∠BAD=90°,
∵AB=9,tan∠ADB=![]() ,
,
∴AD=12,
过F作FH⊥AD于H,
∵tan∠ADB=![]() ,
,
∴设DH=4x,FH=3x,
∴DF=5x,
∵∠BEF=90°,
∴∠ABE+∠AEB=∠AEB+∠HEF=90°,
∴∠ABE=∠HEF,
在△ABE与△HEF中,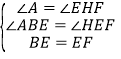
∴△ABE≌△HEF,
∴AE=HF=3x,EH=AB=9,
∴DH﹣AE=AD+EH=4x﹣3x=12+9=21,
∴x=21,
∴DF=5x=105,
综上所述,线段DF的长为![]() 或105.
或105.
故答案为:![]() 或105.
或105.




 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
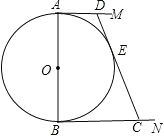
【题目】如图,⊙O的直径是AB=12cm,AM、BN是它的两条切线,DE与⊙O相切于点E,并与AM、BN分别相交于D、C两点,设AD=x,BC=y,则y与x的函数解析式为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是 ( )
A. “打开电视机,正在播放《新闻联播》”是必然事件
B. 天气预报“明天降水概率 50%”,是指明天有一半的时间会下雨
C. 数据 6,6,7,7,8 的中位数与众数均为 7
D. 甲、乙两人在相同的条件下各射击 10 次,他们成绩的平均数相同,方差分别是 S 甲=0.3,S 乙=0.4,则甲的成绩 更稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
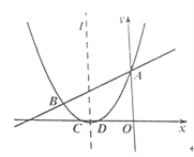
【题目】如图,抛物线 y=![]() x+bx+c 与直线 y=
x+bx+c 与直线 y= ![]() x+3 交于 A,B 两点,点 A 在 y 轴上,抛物线交 x 轴于 C、D 两点,已知 C(-3,0).
x+3 交于 A,B 两点,点 A 在 y 轴上,抛物线交 x 轴于 C、D 两点,已知 C(-3,0).
(1)求抛物线的解析式
(2)在抛物线对称轴 l 上找一点 M,使|MB 一 MD|的值最大。请求出点 M 的坐标及这个最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系 xOy 中,已知正比例函数 y1=﹣2x 的图象与反比例函数 y2=![]() 的图象交于 A(﹣1,a),B 两点.
的图象交于 A(﹣1,a),B 两点.
(1)求出反比例函数的解析式及点 B 的坐标;
(2)观察图象,请直接写出满足 y≤2 的取值范围;
(3)点 P 是第四象限内反比例函数的图象上一点,若△POB 的面积为 1,请直接写出点 P的横坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,阳光下,小亮的身高如图中线段AB所示,他在地面上的影子如图中线段BC所示,线段DE表示旗杆的高,线段FG表示一堵高墙.
(1)请你在图中画出旗杆在同一时刻阳光照射下形成的影子,并用线段表示;
(2)如果小亮的身高AB=1.6m,他的影子BC=2.4m,旗杆的高DE=15m,旗杆与高墙的距离EG=16m,请求出旗杆的影子落在墙上的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,正方形ABCD中,AB=4cm,点P从点D出发沿DA向点A匀速运动,速度是1cm/s,同时,点Q从点A出发沿AB方向,向点B匀速运动,速度是2cm/s,连接PQ、CP、CQ,设运动时间为t(s)(0<t<2)
(1)是否存在某一时刻t,使得PQ∥BD?若存在,求出t值;若不存在,说明理由
(2)设△PQC的面积为s(cm2),求s与t之间的函数关系式;
(3)如图2,连接AC,与线段PQ相交于点M,是否存在某一时刻t,使S△QCM:S△PCM=3:5?若存在,求出t值;若不存在,说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com