
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:①b2>4ac;②方程ax2+bx+c=0的两个根是x1=﹣1,x2=3;③当y>0时,x的取值范围是﹣1<x≤3;④当x>0时,y随x增大而增大.⑤a>-![]() c上述五个结论中正确的有_________(填序号)
c上述五个结论中正确的有_________(填序号)
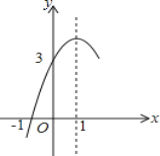
【答案】①②
【解析】
利用抛物线与x轴的交点个数可对①进行判断;利用抛物线的对称性得到抛物线与x轴的另一个交点坐标为(3,0),则可对②进行判断;根据抛物线在x轴上方所对应的自变量的范围可对③进行判断;根据二次函数的性质对④进行判断.由对称轴方程得到b=-2a,然后根据x=-1时函数值为0可得到3a+c=0,则可对⑤进行判断.
∵抛物线与x轴有2个交点,
∴![]() 即
即![]() 所以①正确;
所以①正确;
∵抛物线的对称轴为直线x=1,
而点(1,0)关于直线x=1的对称点的坐标为(3,0),
∴方程![]() 的两个根是
的两个根是![]() 所以②正确;
所以②正确;
∵抛物线与x轴的两点坐标为(1,0),(3,0),
∴当1<x<3时,y>0,所以③错误;
∵抛物线的对称轴为直线x=1,
∴当x<1时,y随x增大而增大,所以④错误;
∵![]() 即b=2a,
即b=2a,
而x=1时,y=0,即ab+c=0,
∴a+2a+c=0,
∴3a+c=0,即![]() ,所以⑤错误;
,所以⑤错误;
故答案为:①②.


科目:初中数学 来源: 题型:
【题目】阅读下列材料:阅读下列材料:在《北京城市总体规划(2004 年—2020 年)》中,房山区被确定为城市发展新区和生态涵养区,承担着首都经济发展、生态涵养、人口疏解和休闲度假等功能.
近年来房山区地区生产总值和财政收入均稳定增长.2011 年房山区地方生产总值是 416.0 亿元;2012 年是科学助力之年,地方生产总值 449.3 亿元,比上一年增长8.0%;2013 年房山努力在区域经济发展上取得新突破,地方生产总值是 481.8 亿元,比上年增长 7.2% ;2014 年房山区域经济稳中提质,完成地方生产总值是 519.3 亿元,比上年增长 7.8%;2015 年房山区统筹推进稳增长,地区生产总值是 554.7 亿元,比上年增长了 6.8%;2016 年经济平稳运行,地区生产总值是 593 亿元,比上年增长了 6.9%.根据以上材料解答下列问题:
(1)选择折线图或条形图将 2011 年到 2016 年的地方生产总值表示出来,并在图中标明相应数据;
(2)根据绘制的统计图中的信息,预估 2017 年房山区地方生产总值是___亿元,你的预估理由是____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正三角形A1B1C1的面积为1,取ΔA1B1C1各边的中点A2、B2、C2,作第二个正三角形A2B2C2,再取ΔA2B2C2各边的中点A3、B3、C3,作第三个正三角形A3B3C3,……,则第4个正三角形A4B4C4的面积是__________;第n个正三角形AnBnCn的面积是_____________。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E、F分别在边BC、DC上,AE、AF分别交BD于点M、N,连接CN、EN,且CN=EN.下列结论:①AN=EN,AN⊥EN;②BE+DF=EF;③![]() ;④图中只有4对相似三角形,其中正确结论的个数是( )
;④图中只有4对相似三角形,其中正确结论的个数是( )
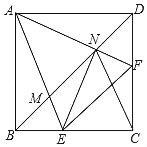
A. 4B. 3C. 2D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD的边AB上任取一点E,作EF⊥AB交BD于点F,取FD的中点G,连接EG、CG,如图(1),易证 EG=CG且EG⊥CG.
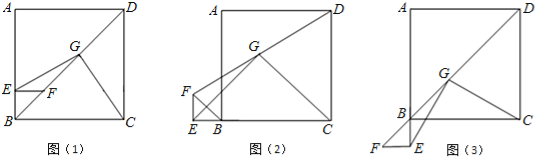
(1)将△BEF绕点B逆时针旋转90°,如图(2),则线段EG和CG有怎样的数量关系和位置关系?请直接写出你的猜想.
(2)将△BEF绕点B逆时针旋转180°,如图(3),则线段EG和CG又有怎样的数量关系和位置关系?请写出你的猜想,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
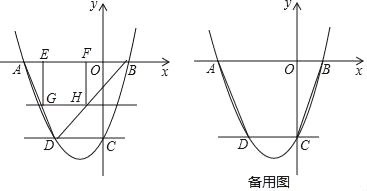
【题目】如图,已知抛物线y=ax2+bx﹣3与x轴交于点A(﹣3,0)和点B(1,0),交y轴于点C,过点C作CD∥x轴,交抛物线于点D.
(1)求抛物线的解析式;
(2)若直线y=m(﹣3<m<0)与线段AD、BD分别交于G、H两点,过G点作EG⊥x轴于点E,过点H作HF⊥x轴于点F,求矩形GEFH的最大面积;
(3)若直线y=kx+1将四边形ABCD分成左、右两个部分,面积分别为S1,S2,且S1:S2=4:5,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
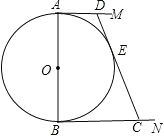
【题目】如图,⊙O的直径是AB=12cm,AM、BN是它的两条切线,DE与⊙O相切于点E,并与AM、BN分别相交于D、C两点,设AD=x,BC=y,则y与x的函数解析式为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com