
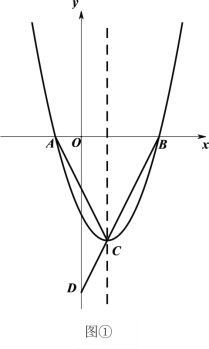
【题目】如图①,二次函数![]() 的图像与
的图像与![]() 轴交于
轴交于![]() 、
、![]() 两点(点
两点(点![]() 在
在![]() 的左侧),顶点为
的左侧),顶点为![]() ,连接
,连接![]() 并延长交
并延长交![]() 轴于点
轴于点![]() ,若
,若![]() .
.
(1)求二次函数的表达式;
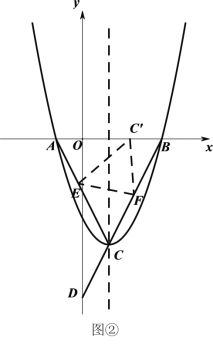
(2)在![]() 轴上方有一点
轴上方有一点![]() ,
,![]() ,且
,且![]() ,连接
,连接![]() 并延长交抛物线于点
并延长交抛物线于点![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)如图②,折叠△![]() ,使点
,使点![]() 落在线段
落在线段![]() 上的点
上的点![]() 处,折痕为
处,折痕为![]() .若△
.若△![]() 有一条边与
有一条边与![]() 轴垂直,直接写出此时点
轴垂直,直接写出此时点![]() 的坐标.
的坐标.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]() 、
、![]()
【解析】
(1)函数的对称轴为x![]() 1,BC=2CD,xB=3xC=3,即B的坐标为(3,0),即可求解;
1,BC=2CD,xB=3xC=3,即B的坐标为(3,0),即可求解;
(2)易证HMA≌△ANC(AAS),则AM=NC=2,MH=AN=4,可求出点H的坐标和直线CH的表达式,将该表达式与二次函数表达式联立,即可求解;
(3)分C'F⊥x轴、EC'⊥x轴,两种情况求解即可.
(1)函数的对称轴为x![]() 1,BC=2CD,xB=3xC=3,即B的坐标为(3,0),将点B的坐标代入二次函数表达式得:
1,BC=2CD,xB=3xC=3,即B的坐标为(3,0),将点B的坐标代入二次函数表达式得:
0=a×32﹣2a×3﹣3,解得:a=1.
故二次函数的表达式为:y=x2﹣2x﹣3…①,则顶点C的坐标为(1,﹣4),令y=0,则x=﹣1或3,即点A的坐标为(﹣1,0);
(2)过点A作MN∥y轴,分别过点H、C作HM⊥MN、CN⊥MN于点M、N,如图1.
∵∠MAH+∠NAC=90°,∠NAC+∠ACN=90°,∴∠MAH=∠ACN,∠HMA=∠CNA=90°,AC=AH,∴△HMA≌△ANC(AAS),∴AM=NC=2,MH=AN=4,∴点H的坐标为(3,2),设直线HC的解析式为:y=mx+n,把H、C的坐标代入得:![]() ,解得:
,解得:![]() ,故直线CH的表达式为:y=3x﹣7…②,联立①②并解得:
,故直线CH的表达式为:y=3x﹣7…②,联立①②并解得:![]() 或
或![]() ,即点P的坐标为(4,5);
,即点P的坐标为(4,5);
(3)①当C'F⊥x轴,设:函数对称轴交x轴于点G,如图2,则tan∠GBC![]() ,设:BC'=x,则FC'=2x=FC,则BF
,设:BC'=x,则FC'=2x=FC,则BF![]() x,BC=BF+CF=2x
x,BC=BF+CF=2x![]() ,即:x=10﹣4
,即:x=10﹣4![]() ,∴点C'的坐标为(4
,∴点C'的坐标为(4![]() 7,0);
7,0);


②当EC'⊥x轴,同理可得点C'的坐标为:(9﹣4![]() ,0).
,0).
综上所述:点C'的坐标为(4![]() 7,0)或(9﹣4
7,0)或(9﹣4![]() ,0).
,0).


科目:初中数学 来源: 题型:
【题目】如图,正三角形A1B1C1的面积为1,取ΔA1B1C1各边的中点A2、B2、C2,作第二个正三角形A2B2C2,再取ΔA2B2C2各边的中点A3、B3、C3,作第三个正三角形A3B3C3,……,则第4个正三角形A4B4C4的面积是__________;第n个正三角形AnBnCn的面积是_____________。

查看答案和解析>>
科目:初中数学 来源: 题型:
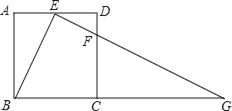
【题目】如图,在正方形ABCD中,E、F分别是边AD、CD上的点,AE=ED,DF:DC=1:4,连接EF并延长交BC的延长线于点G.
(1)求证:△ABE∽△DEF;
(2)若正方形的边长为10,求BG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
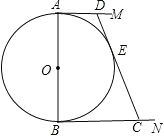
【题目】如图,⊙O的直径是AB=12cm,AM、BN是它的两条切线,DE与⊙O相切于点E,并与AM、BN分别相交于D、C两点,设AD=x,BC=y,则y与x的函数解析式为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是 ( )
A. “打开电视机,正在播放《新闻联播》”是必然事件
B. 天气预报“明天降水概率 50%”,是指明天有一半的时间会下雨
C. 数据 6,6,7,7,8 的中位数与众数均为 7
D. 甲、乙两人在相同的条件下各射击 10 次,他们成绩的平均数相同,方差分别是 S 甲=0.3,S 乙=0.4,则甲的成绩 更稳定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com