
【题目】已知,AB和AC是![]() 的两条弦,
的两条弦,![]() ,M、N分别是AB、AC的中点,则
,M、N分别是AB、AC的中点,则![]() 的度数为______.
的度数为______.
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=900,∠B=∠E=300.
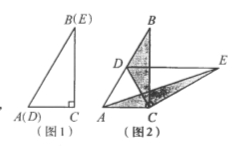


(1)操作发现如图2,固定△ABC,使△DEC绕点C旋转。当点D恰好落在BC边上时,填空:线段DE与AC的位置关系是 ;
② 设△BDC的面积为S1,△AEC的面积为S2。则S1与S2的数量关系是 。
(2)猜想论证
当△DEC绕点C旋转到图3所示的位置时,小明猜想(1)中S1与S2的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC,CE边上的高,请你证明小明的猜想。
(3)拓展探究
已知∠ABC=600,点D是其角平分线上一点,BD=CD=4,OE∥AB交BC于点E(如图4),若在射线BA上存在点F,使S△DCF =S△BDC,请直接写出相应的BF的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有下列四个条件:①AB=BC,②∠ABC=90![]() ,③AC=BD,④AC⊥BD.从中选取两个作为补充条件,使□BCD为正方形(如图).现有下列四种选法,其中错误的是 ( )
,③AC=BD,④AC⊥BD.从中选取两个作为补充条件,使□BCD为正方形(如图).现有下列四种选法,其中错误的是 ( )
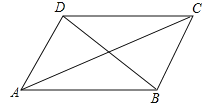
A. ②③ B. ②④ C. ①② D. ①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校同学组织了一次经典朗读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
甲 |
|
|
|
|
|
|
|
|
|
|
乙 |
|
|
|
|
|
|
|
|
|
|
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是![]() 分2,则成绩较为整齐的是 队.
分2,则成绩较为整齐的是 队.
查看答案和解析>>
科目:初中数学 来源: 题型:
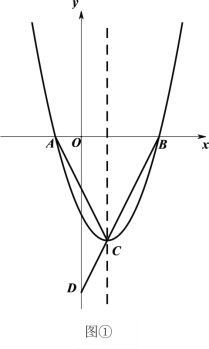
【题目】如图①,二次函数![]() 的图像与
的图像与![]() 轴交于
轴交于![]() 、
、![]() 两点(点
两点(点![]() 在
在![]() 的左侧),顶点为
的左侧),顶点为![]() ,连接
,连接![]() 并延长交
并延长交![]() 轴于点
轴于点![]() ,若
,若![]() .
.
(1)求二次函数的表达式;
(2)在![]() 轴上方有一点
轴上方有一点![]() ,
,![]() ,且
,且![]() ,连接
,连接![]() 并延长交抛物线于点
并延长交抛物线于点![]() ,求点
,求点![]() 的坐标;
的坐标;
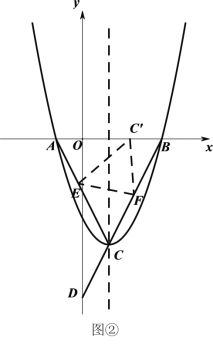
(3)如图②,折叠△![]() ,使点
,使点![]() 落在线段
落在线段![]() 上的点
上的点![]() 处,折痕为
处,折痕为![]() .若△
.若△![]() 有一条边与
有一条边与![]() 轴垂直,直接写出此时点
轴垂直,直接写出此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
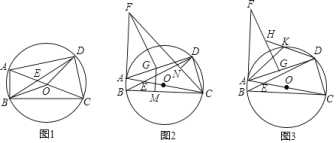
【题目】已知,四边形ABCD内接于![]() ,对角线AC和BD相交于点E,AC是
,对角线AC和BD相交于点E,AC是![]() 的直径.
的直径.
![]() 如图1,连接OB和OD,求证:
如图1,连接OB和OD,求证:![]() ;
;
![]() 如图2,延长BA到点F,使
如图2,延长BA到点F,使![]() ,在AD上取一点G,使
,在AD上取一点G,使![]() ,连接FG和FC,过点G作
,连接FG和FC,过点G作![]() ,垂足为M,过点D作
,垂足为M,过点D作![]() ,垂足为N,求
,垂足为N,求![]() 的值;
的值;
![]() 如图3,在
如图3,在![]() 的条件下,点H为FG的中点,连接DH交
的条件下,点H为FG的中点,连接DH交![]() 于点K,连接AK,若
于点K,连接AK,若![]() ,
,![]() ,求线段BC的长.
,求线段BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
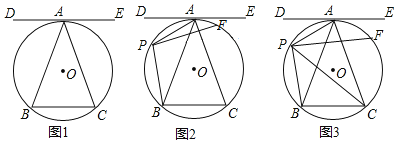
【题目】.如图,⊙O是△ABC的外接圆,直线DE是⊙O的切线,点A为切点,DE∥BC;
(1)如图1.求证:AB=AC;
(2)如图2.点P是弧AB上一动点,连接PA、PB,作PF⊥PB,垂足为点P,PF交⊙O于点F, 求证:∠BAC=2∠APF;
(3)如图3.在(2)的条件下,连接PC,PA=![]() ,PB=
,PB=![]() ,PC=
,PC=![]() ,求线段PF的长.
,求线段PF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
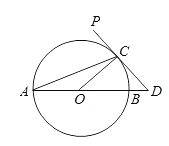
【题目】如图,AB 为⊙O 的直径,PD 切⊙O 于点 C,交 AB 的延长线于点 D,且∠D=2∠A.
(1)求∠D 的度数;
(2)若⊙O 的半径为 m,求 BD 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
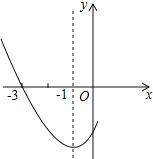
【题目】如图,是二次函数![]() 图象的一部分,其对称轴是
图象的一部分,其对称轴是![]() ,且过点
,且过点![]() ,下列说法:
,下列说法:![]() ;
;![]() ;
;![]() ;
;![]() 若
若![]() ,
,![]() 是抛物线上两点,则
是抛物线上两点,则![]() ,其中正确的有
,其中正确的有![]()
![]()
A. 1个
B. 2个
C. 3个
D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com