【题目】如图，四边形
为矩形，四边形
为菱形．
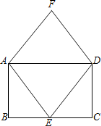
求证：
；
试探究：当矩形边长满足什么关系时，菱形为正方形？请说明理由．
【答案】(1)见解析;(2)见解析.
【解析】
（1）根据矩形的性质可得∠B=∠C=90°，AB=DC，根据菱形的四条边都相等可得AE=DE，然后利用“HL”证明Rt△ABERt△DCE即可；（2）BC=2AB时，菱形AEDF为正方形．根据全等三角形对应边相等可得BE=CE，然后求出AB=BE，从而求出∠BAE=∠AEB=45°，同理可得∠DEC=45°，然后求出∠AED=90°，最后根据有一个角是90°的菱形是正方形即可证得结论．
证明：∵四边形
为矩形，
∴
，
，
∵四边形
为菱形，
∴
，
在
和
中，
，
∴
；
当
时，菱形为正方形．
理由：∵
，
∴
，
，
又∵，
∴
，
∴
，
同理可得，
，
∵
，
∴
，
∴菱形是正方形．
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】作图题：如图在矩形ABCD中，已知AD=10，AB=6，用直尺和圆规在AD上找一点E（保留作图痕迹），使EC平分∠BED，并求出tan∠BEC的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读下面材料，完成
题．
数学课上，老师出示了这样一道题：
如图1，在
中，
点
在
上，点
在
上，
．点
在
延长线上，连接
．探究线段
与
的数量关系并证明．
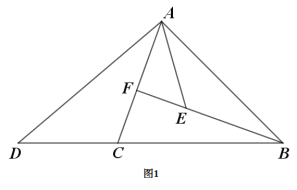
同学们经过思考后，交流了自己的想法：
小明：“通过观察和度量，发现
与
相等．”
小亮：“通过观察和度量，发现
与
也相等．”
小伟：“通过边角关系构造辅助线，经过进一步推理， 可以得到线段与的数量关系．”
老师：“保留原题条件，延长图1中的
与相交于点
(如图2)，若知道
与
的数量关系，可以求出
的值．”
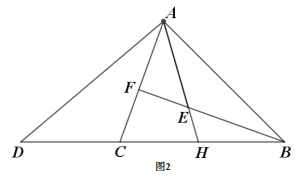
（1）求证：
；
（2）求
的值(用含
的式子表示)；
（3）如图2，若
则的值为 (用含的式子表示)．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直线y＝
x+a与x轴交于点A（4，0），与y轴交于点B，抛物线y＝x2+bx+c经过点A，B．点M（m，0）为x轴上一动点，过点M且垂直于x轴的直线分别交直线AB及抛物线于点P，N．
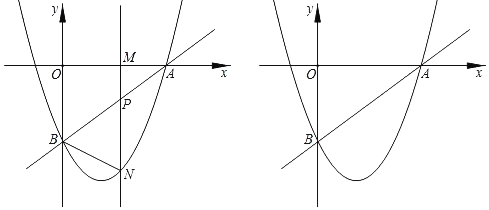
（1）填空：点B的坐标为 ，抛物线的解析式为 ；
（2）当点M在线段OA上运动时（不与点O，A重合），
①当m为何值时，线段PN最大值，并求出PN的最大值；②求出使△BPN为直角三角形时m的值；
（3）若抛物线上有且只有三个点N到直线AB的距离是h，请直接写出此时由点O，B，N，P构成的四边形的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】一名在校大学生利用“互联网+”自主创业，销售一种产品，这种产品的成本价10元/件，已知销售价不低于成本价，且物价部门规定这种产品的销售价不高于16元/件，市场调查发现，该产品每天的销售量
（件
与销售价
（元/件）之间的函数关系如图所示．
（1）求与之间的函数关系式，并写出自变量的取值范围；
（2）求每天的销售利润W（元与销售价（元/件）之间的函数关系式，并求出每件销售价为多少元时，每天的销售利润最大？最大利润是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】一声汽笛长鸣，火车开进了蔡家崖．这是我省吕梁革命老区人民期盼已久的客运列车．蔡家崖列车的开通．带动老区驶入了发展红色旅游的快车进．某旅行社对去年“国庆”期间到吕梁观光的游客的出行方式进行了随机抽样调查，整理后绘制了两幅统计图（尚不完整）．根据图中信息，回答下列问题：
（1）求本次抽样调查的总人数：
（2）补全条形统计图；
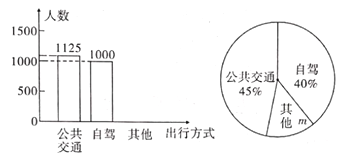
（3）扇形统计图中“其他”部分扇形的圆心角度数为____；
（4）去年“国庆”期问到吕梁观光的旅游者为275万人，则选择自驾方式出行的有多少万人．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如今很多初中生喜欢购买饮品饮用，既影响身体健康又给家庭增加不必要的开销，为此九（2）班数学兴趣小组对本班同学天饮用饮品的情况进行了调查，发现大致可分为四种：A非碳酸饮料，B瓶装矿泉水，C碳酸饮料，D白开水．
根据统计结果绘制如下两个统计图，根据统计图提供的信息解答下列问题：
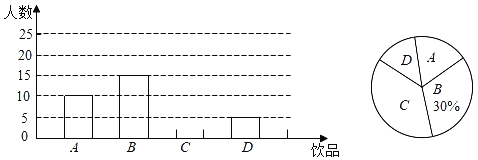
（1）九（2）班级有多少名同学？并补全条形统计图；
（2）若该班同学每人每天只饮用一种饮品（每种仅限一瓶，价格如表），则该班同学每天用于饮品的人均花费是多少元？
饮品名称 | 白开水 | 瓶装矿泉水 | 碳酸饮料 | 非碳酸饮料 |
平均价格（元/瓶） | 0 | 2 | 3 | 4 |
（3）为了养成良好的生活习惯，班主任决定在饮用白开水的5名同学（其中有两位班长记为a，b，其余三位记为c，d，e）中随机抽取2名作良好习惯监督员，请用列表法或画树状图的方法，求出抽到的2名同学都不是班长的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某学校为了防控新型冠状病毒，购买了甲、乙两种消毒液进行校园环境消毒．己知学校第一次购买了甲种消毒液40瓶和乙种消毒液60瓶，共花费3 600元；第二次购买了甲种消毒液60瓶和乙种消毒液40瓶，共花费3 400元．
（1）每瓶甲种消毒液和每瓶乙种消毒液的价格分别是多少元?
（2）学校准备第三次购买这两种消毒液，其中甲种消毒液比乙种消毒液多10瓶，并且总花费不超过3 500元，最多能购买多少瓶甲种消毒液?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
