
【题目】图①、图②均是5×6的正方形网格,每个小正方形的顶点称为格点,小正方形的边长为1,点A、E、F均在格点上.在图①、图②中,只用无刻度的直尺,在给定的网格中按要求画图,所画图形的顶点均在格点上,不要求写出画法.
(1)在图①中画一个正方形ABCD,使其面积为5.
(2)在图②中画一个等腰△EFG,使EF为其底边.

科目:初中数学 来源: 题型:
【题目】已知四边形ABCD是正方形,△DEF是等腰直角三角形,DE=DF,M是EF的中点.

(1)如图1,当点E在AB上时,求证:点F在直线BC上.
(2)如图2,在(1)的条件下,当CM=CF时,求证:∠CFM=22.5°
(3)如图3,当点E在BC上时,若CM=2,则BE的长为 (直接写出结果)(注:等腰直角三角形三边之比为1:1:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂甲、乙两个部门各有员工200人,为了解这两个部门员工的生产技能情况,相关部门进行了抽样调查,过程如下.
从甲、乙两个部门各随机抽取20名员工,进行了生产技能测试,测试成绩(百分制,单位:分)如下:
甲:78 86 74 81 75 76 87 70 75 90
75 79 81 70 75 80 85 70 83 77
乙:92 71 83 81 72 81 91 83 75 82
80 81 69 81 73 74 82 80 70 59
整理、描述数据
按如下分数段整理、描述这两组样本数据:
成绩x 人数 部门 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
甲 | 0 | 0 | 12 | 7 | 1 |
乙 | 1 | 1 | 6 |
|
|
(说明:成绩80分及以上为生产技能优秀,70﹣﹣79分为生产技能良好,60﹣﹣69分为生产技能合格)
根据上述表格绘制甲、乙两部门员工成绩的频数分布图.

分析数据
两组样本数据的平均数、中位数、众数如下表所示:
部门 | 平均数 | 中位数 | 众数 |
甲 | 78.35 | 77.5 | 75 |
乙 | 78 | 80.5 | 81 |
(1)请将上述不完整的统计表和统计图补充完整;
(2)请根据以上统计过程进行下列推断;
①估计乙部门生产技能优秀的员工人数是多少;
②你认为甲、乙哪个部门员工的生产技能水平较高,说明理由.(至少从两个不同的角度说明推断的合理性)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】沿海城市A接到台风警报,在该市正南方向130km的B处有一台风中心,沿BC方向以15km/h的速度向D移动,已知城市A到BC的距离AD=50km,那么台风中心经过多长时间从B点移到D点?如果在距台风中心30km的圆形区域内都将有受到台风的破坏的危险,正在D点休闲的游人在接到台风警报后的几小时内撤离才可脱离危险?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,其顶点坐标为A(﹣1,﹣3),与x轴的一个交点为B(﹣3,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:①abc>0;②不等式ax2+(b﹣m)x+c﹣n<0的解集为﹣3<x<﹣1;③抛物线与x轴的另一个交点是(3,0);④方程ax2+bx+c+3=0有两个相等的实数根;其中正确的是( )
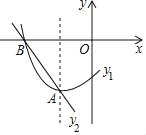
A. ①③ B. ②③ C. ③④ D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc<0;②b<a+c;③4a+2b+c>0;④2c<3b;⑤a+b<m(am+b)(m≠1且为实数),其中正确的个数是( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(![]() ,0),B(0,4),则点B4的坐标为_____,点B2017的坐标为_____.
,0),B(0,4),则点B4的坐标为_____,点B2017的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E、F是正方形ABCD的边AD上有两个动点,满足AE=DF,连接CF交BD于G,连接BE交AG于点H,若正方形的边长为3,则线段DH长度的最小值是_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com