
【题目】某工厂甲、乙两个部门各有员工200人,为了解这两个部门员工的生产技能情况,相关部门进行了抽样调查,过程如下.
从甲、乙两个部门各随机抽取20名员工,进行了生产技能测试,测试成绩(百分制,单位:分)如下:
甲:78 86 74 81 75 76 87 70 75 90
75 79 81 70 75 80 85 70 83 77
乙:92 71 83 81 72 81 91 83 75 82
80 81 69 81 73 74 82 80 70 59
整理、描述数据
按如下分数段整理、描述这两组样本数据:
成绩x 人数 部门 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
甲 | 0 | 0 | 12 | 7 | 1 |
乙 | 1 | 1 | 6 |
|
|
(说明:成绩80分及以上为生产技能优秀,70﹣﹣79分为生产技能良好,60﹣﹣69分为生产技能合格)
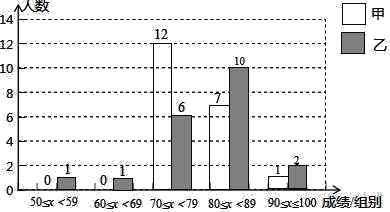
根据上述表格绘制甲、乙两部门员工成绩的频数分布图.

分析数据
两组样本数据的平均数、中位数、众数如下表所示:
部门 | 平均数 | 中位数 | 众数 |
甲 | 78.35 | 77.5 | 75 |
乙 | 78 | 80.5 | 81 |
(1)请将上述不完整的统计表和统计图补充完整;
(2)请根据以上统计过程进行下列推断;
①估计乙部门生产技能优秀的员工人数是多少;
②你认为甲、乙哪个部门员工的生产技能水平较高,说明理由.(至少从两个不同的角度说明推断的合理性)
【答案】(1)见解析;(2)①120人;②甲或乙.
【解析】
(1)根据题干数据整理即可得;
(2)①总人数乘以样本中优秀的人数所占比例;②根据中位数和众数等意义解答可得.
解:(1)补全图表如下:
成绩x 人数 部门 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
甲 | 0 | 0 | 12 | 7 | 1 |
乙 | 1 | 1 | 6 | 10 | 2 |
(2)①估计乙部门生产技能优秀的员工人数是200×![]() =120人;
=120人;
②甲或乙,
1°、甲部门生产技能测试中,平均分较高,表示甲部门员工的生产技能水平较高;
2°、甲部门生产技能测试中,没有技能不合格的员工,表示甲部门员工的生产技能水平较高;
或1°、乙部门生产技能测试中,中位数较高,表示乙部门员工的生产技能水平较高;
2°、乙部门生产技能测试中,众数较高,表示乙部门员工的生产技能水平较高.


科目:初中数学 来源: 题型:
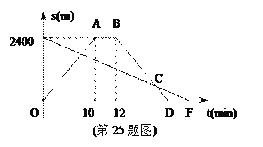
【题目】小明从家骑自行车出发,沿一条直路到相距2400m的邮局办事,小明出发的同时,他的爸爸以96m/min速度从邮局同一条道路步行回家,小明在邮局停留2min后沿原路以原速返回,设他们出发后经过t min时,小明与家之间的距离为s1m,小明爸爸与家之间的距离为s2 m,图中折线OABD、线段EF分别表示s1、s2与t之间的函数关系的图象。
(1)求s2与t之间的函数关系式;
(2)小明从家出发,经过多长时间在返回途中追上爸爸?这时他们距离家还有多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,∠A=30°.

(1)用尺规作图作AB边上的中垂线DE,交AC于点D,交AB于点E.(保留作图痕迹,不要求写作法和证明);
(2)连接BD,求证:BD平分∠CBA.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究:如图①,△ABC是等边三角形,在边AB、BC的延长线上截取BM=CN,连结MC、AN,延长MC交AN于点P.
(1)求证:△ACN≌△CBM;
(2)∠CPN= °;(给出求解过程)
(3)应用:将图①的△ABC分别改为正方形ABCD和正五边形ABCDE,如图②、③,在边AB、BC的延长线上截取BM=CN,连结MC、DN,延长MC交DN于点P,则图②中∠CPN= °;(直接写出答案)
(4)图③中∠CPN= °;(直接写出答案)
(5)拓展:若将图①的△ABC改为正n边形,其它条件不变,则∠CPN= °(用含n的代数式表示,直接写出答案).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A的坐标是(﹣2,3),点B的坐标是(1,﹣1),连接AB,点C是坐标轴上任意一点,则使△ABC为等腰三角形的点C共有_____个.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①、图②均是5×6的正方形网格,每个小正方形的顶点称为格点,小正方形的边长为1,点A、E、F均在格点上.在图①、图②中,只用无刻度的直尺,在给定的网格中按要求画图,所画图形的顶点均在格点上,不要求写出画法.
(1)在图①中画一个正方形ABCD,使其面积为5.
(2)在图②中画一个等腰△EFG,使EF为其底边.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某景区的两个景点A、B处于同一水平地面上、一架无人机在空中沿MN方向水平飞行进行航拍作业,MN与AB在同一铅直平面内,当无人机飞行至C处时、测得景点A的俯角为45°,景点B的俯角为30°,此时C到地面的距离CD为100米,则两景点A、B间的距离为__米(结果保留根号).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com