
����Ŀ��̽������ͼ�٣���ABC�ǵȱ������Σ��ڱ�AB��BC���ӳ����Ͻ�ȡBM=CN������MC��AN���ӳ�MC��AN�ڵ�P��
��1����֤����ACN�ա�CBM��
��2����CPN= ���������������̣�
��3��Ӧ�ã���ͼ�ٵġ�ABC�ֱ��Ϊ������ABCD���������ABCDE����ͼ�ڡ��ۣ��ڱ�AB��BC���ӳ����Ͻ�ȡBM=CN������MC��DN���ӳ�MC��DN�ڵ�P����ͼ���С�CPN= ������ֱ��д���𰸣�
��4��ͼ���С�CPN= ������ֱ��д���𰸣�
��5����չ������ͼ�ٵġ�ABC��Ϊ��n���Σ������������䣬���CPN= �����ú�n�Ĵ���ʽ��ʾ��ֱ��д���𰸣���

���𰸡���1������������2��120����3��90����4��72����5��![]() .
.
��������
��1�����õȱ������ε����ʵõ�BC=AC����ACB=��ABC���Ӷ��õ���ACN�ա�CBM.
��2������ȫ�������ε����ʵõ���CAN=��BCM�������������ε���ǵ������������ڵ������ڽǵĺͣ��������.
��3�����������Σ���������Σ������ʵõ�BC=DC����ABC=��BCD���Ӷ��жϳ���DCN�ա�CBM��������ȫ�������ε����ʵõ���CDN=��BCM���������ڽǺͶ������ɵõ���.
��4���ɣ�3���ķ������ɵõ���.
��5�������������Σ����ı��Σ�������Σ��ֱ������CPN�Ķ���������Ĺ�ϵʽ�����ɵõ���.
��1���ߡ�ABC�ǵȱ������Σ�
��BC=AC����ACB=��BAC=��ABC=60![]() ��
��
���ACN=��CBM=120![]() ��
��
�ڡ�CAN�͡�CBM�У�
 ��
��
���ACN�ա�CBM.
��2���ߡ�ACN�ա�CBM.
���CAN=��BCM��
�ߡ�ABC=��BMC+��BCM����BAN=��BAC+��CAN��
���CPN=��BMC+��BAN
=��BMC+��BAC+��CAN
=��BMC+��BAC+��BCM
=��ABC+��BAC
=60![]() +60
+60![]() ,
,
=120![]() ��
��
�ʴ�Ϊ��120.
��3�����ȱ������λ��������Σ�
���ı���ABCD�������Σ�
��BC=DC����ABC=��BCD=90![]() ��
��
���MBC=��DCN=90![]() ��
��
�ڡ�DCN�͡�CBM�У�
 ��
��
���DCN�ա�CBM��
���CDN=��BCM��
�ߡ�BCM=��PCN��
���CDN=��PCN��
��Rt��DCN����CDN+��CND=90![]() ��
��
���PCN+��CND=90![]() ��
��
���CPN=90![]() ��
��
�ʴ�Ϊ��90.
��4�����ȱ������λ���������Σ�
���ABC=��DCB=108![]() ��
��
���MBC=��DCN=72![]() ��
��
�ڡ�DCN�͡�CBM�У�
 ��
��
���DCN�ա�CBM��
���BMC=��CND����BCM=��CDN��
�ߡ�BCM=��PCN��
���CND=��PCN��
�ڡ�CDN�У���CDN+��CND=��BCD=108![]() ��
��
���CPN=180![]() -(��CND+��PCN)
-(��CND+��PCN)
=180![]() -(��CND+��CDN)
-(��CND+��CDN)
=180![]() -108
-108![]() ��
��
=72![]() ��
��
�ʴ�Ϊ��72.
��5����������ʱ����CPN=120![]() =
=![]() ��
��
���ı���ʱ����CPN=90![]() =
=![]() ��
��
�������ʱ����CPN=72![]() =
=![]() ��
��
��n����ʱ����CPN=![]() ��
��
�ʴ�Ϊ�� ![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���߶�![]() �Ƶ�
�Ƶ�![]() ˳ʱ����תһ���ĽǶȵõ��߶�
˳ʱ����תһ���ĽǶȵõ��߶�![]() ��
��
��1����ֱ�ߺ�Բ��������ת����![]() ����д������������ͼ�ۼ�����
����д������������ͼ�ۼ�����
��2������![]() ��
��![]() ��
��![]() ��
��![]() ������һ������������������߶�
������һ������������������߶�![]() ɨ���������������������ĸ�����ߣ��߶εij�����
ɨ���������������������ĸ�����ߣ��߶εij�����![]() ��
��![]() ��
��![]() ����ʾ���ǵĶ�������
����ʾ���ǵĶ�������![]() ��
��![]() ��
��![]() ����ʾ���������ӵ�������________��
����ʾ���������ӵ�������________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2016�����������У��Ͷ����ʹ���ֻ��Ϳ����õĹ���������ij��Ӫ��Ϊ����侭Ӫ��AƷ�ƹ����������г�ռ���ʣ������շ������µ�����һ���У�ͬһ���˵�һ��ʹ�õij��Ѱ�0.5Ԫ��ȡ��ÿ����һ�Σ����γ��Ѿͱ��ϴγ��Ѽ���0.1Ԫ����6�ο�ʼ�������ó���ѣ������շѱ����£�
ʹ�ô��� | 0 | 1 | 2 | 3 | 4 | 5(��5������) |
�ۼƳ��� | 0 | 0.5 | 0.9 |
|
| 1.5 |
ͬʱ���ʹ��շѷ������������ij��У100��ʦ����һ����ʹ��AƷ�ƹ�����������Ը���õ��������ݣ�
ʹ�ô��� | 0 | 1 | 2 | 3 | 4 | 5 |
���� | 5 | 15 | 10 | 30 | 25 | 15 |
������д��![]() ��ֵ��
��ֵ��
��������֪��У��5000��ʦ������AƷ�ƹ�������Ͷ�Ÿ�Уһ��ķ���Ϊ5800Ԫ���Թ��ƣ��շѵ�������Ӫ���ڸ�УͶ��AƷ�ƹ��������ܷ����? ˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�ȱߡ�ABC�ı߳�Ϊ12��D��AB�ϵĶ��㣬��D��DE��BC�ڵ�E����E��EF��AC�ڵ�F����F��FG��AB�ڵ�G.��G��D�غ�ʱ��AD�ij��ǣ� ��

A.9B.8C.4D.3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����ס����������Ÿ���Ա��200�ˣ�Ϊ�˽�����������Ա�������������������ز��Ž����˳������飬�������£�
�Ӽס����������Ÿ������ȡ20��Ա�����������������ܲ��ԣ����Գɼ����ٷ��ƣ���λ���֣����£�
�ף�78����86����74����81����75����76����87����70����75����90��
75����79����81����70����75����80����85����70����83����77
�ң�92����71����83����81����72����81����91����83����75����82
��80����81����69����81����73����74����82����80����70����59
��������������
�����·����������������������������ݣ�
�ɼ�x ���� ���� | 50��x��59 | 60��x��69 | 70��x��79 | 80��x��89 | 90��x��100 |
�� | 0 | 0 | 12 | 7 | 1 |
�� | 1 | 1 | 6 | �� �� | �� �� |
��˵�����ɼ�80�ּ�����Ϊ�����������㣬70����79��Ϊ�����������ã�60����69��Ϊ�������ܺϸ�
��������������Ƽס���������Ա���ɼ���Ƶ���ֲ�ͼ��

��������
�����������ݵ�ƽ��������λ�����������±���ʾ��
���� | ƽ���� | ��λ�� | ���� |
�� | 78.35 | 77.5 | 75 |
�� | 78 | 80.5 | 81 |
��1���뽫������������ͳ�Ʊ���ͳ��ͼ����������
��2�����������ͳ�ƹ��̽��������ƶϣ�
�ٹ����Ҳ����������������Ա�������Ƕ��٣�
������Ϊ�ס����ĸ�����Ա������������ˮƽ�ϸߣ�˵�����ɣ������ٴ�������ͬ�ĽǶ�˵���ƶϵĺ����ԣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����үҪΧ��һ�����β�������һ�������㹻����ǽ�������Χ�ɵ����������ܳ�Ӧǡ��Ϊ24�ף�ҪΧ�ɵIJ�����ͼ��ʾ�ľ���ABCD����BC�ߵij�Ϊx�ף�AB�ߵij�Ϊy�ף���y��x֮��ĺ�����ϵʽ��( )

A. y=��2x+24(0<x<12) B. y=��![]() x��12(0<x<24)
x��12(0<x<24)
C. y=2x��24(0<x<12) D. y=![]() x��12(0<x<24)
x��12(0<x<24)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��O��ֱ��Ϊ10�������ABC�ڽ�����O��BD��AC�ڵ�D��AB=8����tan��CBD��ֵ���ڣ�������

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y1=ax2+bx+c��a��0��ͼ���һ���֣��䶥������ΪA����1����3������x���һ������ΪB����3��0����ֱ��y2=mx+n��m��0���������߽���A��B���㣬���н��ۣ���abc��0���ڲ���ʽax2+��b��m��x+c��n��0�Ľ⼯Ϊ��3��x����1������������x�����һ�������ǣ�3��0�����ܷ���ax2+bx+c+3=0��������ȵ�ʵ������������ȷ���ǣ�������
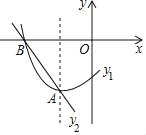
A. �٢� B. �ڢ� C. �ۢ� D. �ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵���У���ȷ���У� ��
�������A+��B-��C=0����ô��ABC��ֱ�������Σ� �������A:��B:��C=5:12:13�����ABC��ֱ�������Σ� ���������������֮��Ϊ![]() �����ABCΪֱ�������Σ���������������߳��ֱ���
�����ABCΪֱ�������Σ���������������߳��ֱ���![]() ��n��2�������ABC��ֱ�������Σ�
��n��2�������ABC��ֱ�������Σ�
A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com