
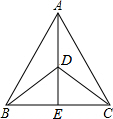
 如图,在△ABC中,AB=AC,DB=DC,AD的延长线交BC于点E,求证:∠BAE=∠CAE.
如图,在△ABC中,AB=AC,DB=DC,AD的延长线交BC于点E,求证:∠BAE=∠CAE. 科目:初中数学 来源: 题型:解答题
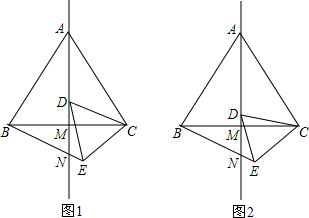
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
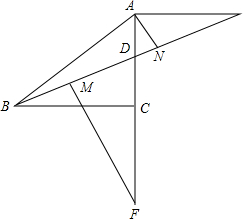 已知:如图,等腰Rt△ABC中,D为AC上一点,AE∥BC交BD延长线于E,AN⊥BE于N,在BE上截取MB=AN,过M作MF⊥BE交AC延长线于F,求证:CF=BC.
已知:如图,等腰Rt△ABC中,D为AC上一点,AE∥BC交BD延长线于E,AN⊥BE于N,在BE上截取MB=AN,过M作MF⊥BE交AC延长线于F,求证:CF=BC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
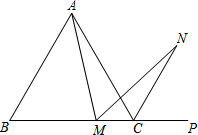 如图,在等边△ABC中,M为BC边上任意一点(不含B、C两点),P为BC延长线上一点,N是∠ACP的平分线上一点.已知∠AMN=60°,求证:AM=NM.
如图,在等边△ABC中,M为BC边上任意一点(不含B、C两点),P为BC延长线上一点,N是∠ACP的平分线上一点.已知∠AMN=60°,求证:AM=NM.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
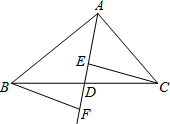 已知命题:如图,在△ABC中,点D是BC的点,作射线AD,在线段AD及其延长线上分别取点E、F,连结CE、BF,则△BDF≌△CDF,判断这个命题是真命题还是假命题?如果是真命题,请给出证明;如果是假命题,请添加一个适当的条件(不添加任何辅助线)使它成为真命题.你所添加的条件是:CE∥BF,并加以证明.
已知命题:如图,在△ABC中,点D是BC的点,作射线AD,在线段AD及其延长线上分别取点E、F,连结CE、BF,则△BDF≌△CDF,判断这个命题是真命题还是假命题?如果是真命题,请给出证明;如果是假命题,请添加一个适当的条件(不添加任何辅助线)使它成为真命题.你所添加的条件是:CE∥BF,并加以证明.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com