
 位于张家界核心景区的贺龙铜像,是我国近百年来最大的铜像.铜像由像体AD和底座CD两部分组成.如图,在Rt△ABC中,∠ABC=70.5°,在Rt△DBC中,∠DBC=45°,且CD=2.3米,求像体AD的高度(最后结果精确到0.1米,参考数据:sin70.5°≈0.943,cos70.5°≈0.334,tan70.5°≈2.824)
位于张家界核心景区的贺龙铜像,是我国近百年来最大的铜像.铜像由像体AD和底座CD两部分组成.如图,在Rt△ABC中,∠ABC=70.5°,在Rt△DBC中,∠DBC=45°,且CD=2.3米,求像体AD的高度(最后结果精确到0.1米,参考数据:sin70.5°≈0.943,cos70.5°≈0.334,tan70.5°≈2.824)  全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:解答题
| 苹果品种 | A | B | C |
| 每辆汽车(吨) | 2.2 | 2.1 | 2 |
| 每吨苹果获利(百元) | 6 | 8 | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
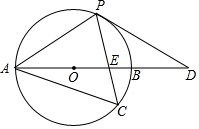 如图,以AB边为直径的⊙O经过点P,C是⊙O上一点,连结PC交AB于点E,且∠ACP=60°,PA=PD.
如图,以AB边为直径的⊙O经过点P,C是⊙O上一点,连结PC交AB于点E,且∠ACP=60°,PA=PD.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
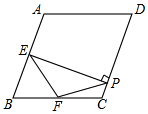 如图,在菱形ABCD中,∠A=100°,E,F分别是边AB和BC的中点,EP⊥CD于点P,则∠FPC的度数为( )
如图,在菱形ABCD中,∠A=100°,E,F分别是边AB和BC的中点,EP⊥CD于点P,则∠FPC的度数为( )| A. | 50° | B. | 55° | C. | 60° | D. | 45° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
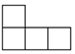 左视图
左视图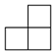
| A. | 5个 | B. | 7个 | C. | 8个 | D. | 9个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
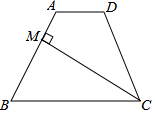 如图,四边形ABCD中,AD∥BC,CM是∠BCD的平分线,且CM⊥AB,M为垂足,AM=$\frac{1}{3}$AB.若四边形ABCD的面积为$\frac{15}{7}$,则四边形AMCD的面积是1.
如图,四边形ABCD中,AD∥BC,CM是∠BCD的平分线,且CM⊥AB,M为垂足,AM=$\frac{1}{3}$AB.若四边形ABCD的面积为$\frac{15}{7}$,则四边形AMCD的面积是1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com