【题目】如图，矩形纸片ABCD中，AB=4，AD=6，点P是边BC上的动点，现将纸片折叠，使点A与点P重合，折痕与矩形边的交点分别为E、F，要使折痕始终与边AB、AD有交点，则BP的取值范围是_________________．

参考答案：

【答案】6-2≤x≤4．

【解析】试题分析：此题需要运用极端原理求解：①BP最小时，F、D重合，由折叠的性质知：AF=PF，在Rt△PFC中，利用勾股定理可求得PC的长，进而可求得BP的值，即BP的最小值；②BP最大时，E、B重合，根据折叠的性质即可得到AB=BP=34，即BP的最大值为4；根据上述两种情况即可得到BP的取值范围．

试题解析：如图：

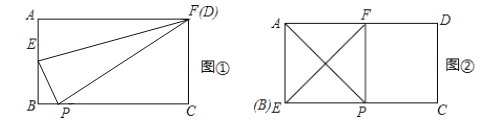
①当F、D重合时，BP的值最小；

根据折叠的性质知：AF=PF=6；

在Rt△PFC中，PF=6，FC=4，则PC=2；

∴BP=xmin=6-2；

②当E、B重合时，BP的值最大；根据折叠的性质即可得到AB=BP=4，即BP的最大值为4；

故答案为：6-2≤x≤4．

关闭