
����Ŀ����ͼ1��������ABCD�У��Խ���AC��BD�ཻ�ڵ�O��AB=13��BD=24��������ABCD���ⲿ��ABΪ�����ȱ������� ABE����F�ǶԽ���BD��һ���㣨��F�����B�غϣ������߶�AF�Ƶ�A˳ʱ�뷽����ת60���õ��߶�AM������FM��

��1����AO�ij���
��2����ͼ2������F���߶�BO�ϣ��ҵ�M��F��C������ͬһ��ֱ����ʱ����֤��AC=![]() AM��
AM��
��3������EM������AEM�����Ϊ40����ֱ��д����AFM���ܳ���
���𰸡���1����5����2����֤�����̼���������3����3![]()
��������
�����������1������RT��OAB�У����ù��ɶ���OA=![]() ��⣻��2�������ı���ABCD�����Σ������AFMΪ�ȱ������Σ���M=��AFM=60�����������MAC=90������Rt��ACM��tan��M=
��⣻��2�������ı���ABCD�����Σ������AFMΪ�ȱ������Σ���M=��AFM=60�����������MAC=90������Rt��ACM��tan��M=![]() �����AC����3���������AEM�ա�ABF��������AEM�����Ϊ40���BF�������ù��ɶ���AF=
�����AC����3���������AEM�ա�ABF��������AEM�����Ϊ40���BF�������ù��ɶ���AF=![]() =
=![]() ���ó���AFM���ܳ�Ϊ3
���ó���AFM���ܳ�Ϊ3![]() ��
��
�����������1�������ı���ABCD�����Σ�
��AC��BD��OB=OD=![]() BD��
BD��
��BD=24��
��OB=12��
��Rt��OAB��
��AB=13��
��OA=![]() =5��
=5��
��2������ͼ2��
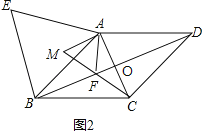
���ı���ABCD�����Σ�
��BD��ֱƽ��AC��
��FA=FC����FAC=��FCA��
����֪AF=AM����MAF=60����
���AFMΪ�ȱ������Σ�
���M=��AFM=60����
����M��F��C������ͬһ��ֱ���ϣ�
���FAC+��FCA=��AFM=60����
���FAC=��FCA=30����
���MAC=��MAF+��FAC=60��+30��=90����
��Rt��ACM����tan��M=![]() ��
��
��tan60��=![]() ��
��
��AC=![]() AM��
AM��
��3������ͼ������EM��
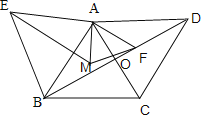
�ߡ�ABE�ǵȱ������Σ�
��AE=AB����EAB=60����
�ɣ�2��֪��AFMΪ�ȱ������Σ�
��AM=AF����MAF=60����
���EAM=��BAF��
����AEM����ABF�� ��
��
���AEM�ա�ABF��SAS����
�ߡ�AEM�����Ϊ40����ABF�ĸ�ΪAO
��![]() BFAO=40��BF=16��
BFAO=40��BF=16��
��FO=BF��BO=16��12=4
AF=![]() =
=![]() ��
��
���AFM���ܳ�Ϊ3![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����д���������ȷ���ǣ� ��
A.��x3��2=x5
B.��2x��2=2x2
C.��x+1��2=x2+1
D.x3x2=x5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������3��3����ͼ������9����ͬ��С��������ɣ�ÿ������ͼ����3��С��������Ϳ����Ӱ���������µ�6���հ�С�������У�������Ҫ��Ϳ����Ӱ��
(1)ѡȡ1��Ϳ����Ӱ��ʹ4����ӰС���������һ����Գ�ͼ�Σ����������ĶԳ�ͼ�Σ�
(2)ѡȡ1��Ϳ����Ӱ��ʹ4����ӰС���������һ�����ĶԳ�ͼ�Σ���������Գ�ͼ�Σ�
(3)ѡȡ2��Ϳ����Ӱ��ʹ5����ӰС���������һ����Գ�ͼ�Σ�
(�뽫����С������������ͼ1��ͼ2��ͼ3�У���ֻ�軭������������һ������)

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ȫƽ����ʽ����79.82�����ѡ����( )
A. (80��0.2)2 B. (100��20.2)2
C. (79��0.8)2 D. (70��9.8)2
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com