
如图,在平面直角坐标系中,直线y=2x+b(b<0)与坐标轴交于A,B两点,与双曲线y=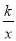 (x>0)交于D点,过点D作DC⊥x轴,垂足为G,连接OD.已知△AOB≌△ACD.
(x>0)交于D点,过点D作DC⊥x轴,垂足为G,连接OD.已知△AOB≌△ACD.
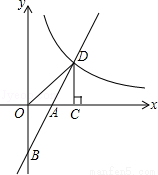
(1)如果b=﹣2,求k的值;
(2)试探究k与b的数量关系,并写出直线OD的解析式.
(1)4;(2)即k与b的数量关系为:k=b2.直线OD的解析式为:y=x.
【解析】
试题分析:(1)首先求出直线y=2x-2与坐标轴交点的坐标,然后由△AOB≌△ACD得到CD=OB,AO=AC,即可求出D坐标,由点D在双曲线y=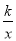 ( x>0)的图象上求出k的值;
( x>0)的图象上求出k的值;
(2)首先直线y=2x+b与坐标轴交点的坐标为A(-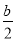 ,0),B(0,b),再根据△AOB≌△ACD得到CD=DB,AO=AC,即可求出D坐标,把D点坐标代入反比例函数解析式求出k和b之间的关系,进而也可以求出直线OD的解析式.
,0),B(0,b),再根据△AOB≌△ACD得到CD=DB,AO=AC,即可求出D坐标,把D点坐标代入反比例函数解析式求出k和b之间的关系,进而也可以求出直线OD的解析式.
试题解析:(1)当b=-2时,
直线y=2x-2与坐标轴交点的坐标为A(1,0),B(0,-2).
∵△AOB≌△ACD,
∴CD=OB,AO=AC,
∴点D的坐标为(2,2).
∵点D在双曲线y=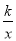 ( x>0)的图象上,
( x>0)的图象上,
∴k=2×2=4.
(2)直线y=2x+b与坐标轴交点的坐标为A(-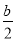 ,0),B(0,b).
,0),B(0,b).
∵△AOB≌△ACD,
∴CD=OB,AO=AC,
∴点D的坐标为(-b,-b).
∵点D在双曲线y=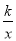 ( x>0)的图象上,
( x>0)的图象上,
∴k=(-b)•(-b)=b2.
即k与b的数量关系为:k=b2.直线OD的解析式为:y=x.
考点:反比例函数综合题.


 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源:2013-2014学年湖南省长沙市九年级下学期期中考试数学试卷(解析版) 题型:选择题
如图,已知点A在反比例函数y= 的图象上,点B在反比例函数y=
的图象上,点B在反比例函数y= (k≠0)的图象上,AB∥x轴,分别过点A、B向x轴作垂线,垂足分别为C、D,若OC=
(k≠0)的图象上,AB∥x轴,分别过点A、B向x轴作垂线,垂足分别为C、D,若OC= OD,则k的值为( )
OD,则k的值为( )

A.10 B.12 C.14 D.16
查看答案和解析>>
科目:初中数学 来源:2013-2014学年浙江省宁波市九年级上学期第一次月考数学试卷(解析版) 题型:解答题
已知抛物线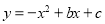 经过点A(3,0),B(-1,0).
经过点A(3,0),B(-1,0).
(1)求抛物线的解析式;
(2)求抛物线的对称轴.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年浙江省宁波市九年级上学期第一次月考数学试卷(解析版) 题型:选择题
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,在下列五个结论中:①2a﹣b<0;②abc<0;③a+b+c<0;④a﹣b+c>0;⑤4a+2b+c>0,错误的个数有( )

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源:2013-2014学年浙江省宁波市九年级上学期期中考试数学试卷(解析版) 题型:解答题
已知二次函数的图象的顶点坐标为(3,-2)且与 轴交与(0,
轴交与(0, )
)
(1)求函数的解析式
(2)当 为何值时,
为何值时, 随
随 增大而增大? 当
增大而增大? 当 为何值时,函数值是非负数?
为何值时,函数值是非负数?
查看答案和解析>>
科目:初中数学 来源:2013-2014学年浙江省丽水市莲都区九年级第一次中考模拟数学试卷(解析版) 题型:选择题
截至2013年第一季度末,浙江省企业养老保险参保人数达8500000人,则数字8500000用科学记数法表示为
A.8.5×106 B.8.5×105 C.0.85×106 D.8.5×107
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com