
ЁОЬтФПЁПвбжЊЁїABCЪЧЕШбќжБНЧШ§НЧаЮЃЌAC=BC=2ЃЌDЪЧБпABЩЯвЛЖЏЕуЃЈAЁЂBСНЕуГ§ЭтЃЉЃЌНЋЁїCADШЦЕуCАДФцЪБеыЗНЯђа§зЊНЧІСЕУЕНЁїCEFЃЌЦфжаЕуEЪЧЕуAЕФЖдгІЕуЃЌЕуFЪЧЕуDЕФЖдгІЕуЃЎ
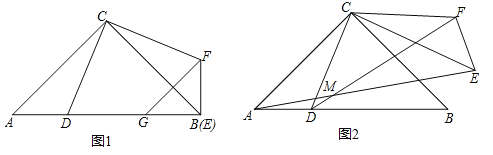
ЃЈ1ЃЉШчЭМ1ЃЌЕБІС=90ЁуЪБЃЌGЪЧБпABЩЯвЛЕуЃЌЧвBG=ADЃЌСЌНгGFЃЎЧѓжЄЃКGFЁЮACЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЕБ90ЁуЁмІСЁм180ЁуЪБЃЌAEгыDFЯрНЛгкЕуMЃЎ
ЂйЕБЕуMгыЕуCЁЂDВЛжиКЯЪБЃЌСЌНгCMЃЌЧѓЁЯCMDЕФЖШЪ§ЃЛ
ЂкЩшDЮЊБпABЕФжаЕуЃЌЕБІСДг90ЁуБфЛЏЕН180ЁуЪБЃЌЧѓЕуMдЫЖЏЕФТЗОЖГЄЃЎ
ЁОД№АИЁПЃЈ1ЃЉжЄУїМћНтЮіЃЛЃЈ2ЃЉЂй135ЁуЃЛЂк![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЪдЬтЗжЮіЃКЃЈ1ЃЉгћжЄУїGFЁЮACЃЌжЛвЊжЄУїЁЯA=ЁЯFGBМДПЩНтОіЮЪЬтЃЎ
ЃЈ2ЃЉЂйЯШжЄУїAЁЂDЁЂMЁЂCЫФЕуЙВдВЃЌЕУЕНЁЯCMF=ЁЯCAD=45ЁуЃЌМДПЩНтОіЮЪЬтЃЎ
ЂкРћгУЂйЕФНсТлПЩжЊЃЌЕуMдквдACЮЊжБОЖЕФЁбOЩЯЃЌдЫЖЏТЗОЖЪЧЛЁCDЃЌРћгУЛЁГЄЙЋЪНМДПЩНтОіЮЪЬтЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉШчЭМ1жаЃЌЁпCA=CBЃЌЁЯACB=90ЁуЃЌЁрЁЯA=ЁЯABC=45ЁуЃЌЁпЁїCEFЪЧгЩЁїCADа§зЊФцЪБеыІСЕУЕНЃЌІС=90ЁуЃЌЁрCBгыCEжиКЯЃЌЁрЁЯCBE=ЁЯA=45ЁуЃЌЁрЁЯABF=ЁЯABC+ЁЯCBF=90ЁуЃЌЁпBG=AD=BFЃЌЁрЁЯBGF=ЁЯBFG=45ЁуЃЌЁрЁЯA=ЁЯBGF=45ЁуЃЌЁрGFЁЮACЃЎ
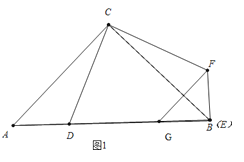
ЃЈ2ЃЉЂйШчЭМ2жаЃЌЁпCA=CEЃЌCD=CFЃЌЁрЁЯCAE=ЁЯCEAЃЌЁЯCDF=ЁЯCFDЃЌЁпЁЯACD=ЁЯECFЃЌЁрЁЯACE=ЁЯCDFЃЌЁп2ЁЯCAE+ЁЯACE=180ЁуЃЌ2ЁЯCDF+ЁЯDCF=180ЁуЃЌЁрЁЯCAE=ЁЯCDFЃЌЁрAЁЂDЁЂMЁЂCЫФЕуЙВдВЃЌЁрЁЯCMF=ЁЯCAD=45ЁуЃЌЁрЁЯCMD=180ЁуЉЁЯCMF=135ЁуЃЎ
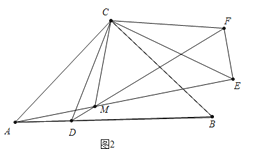
ЂкШчЭМ3жаЃЌOЪЧACжаЕуЃЌСЌНгODЁЂCMЃЎ
ЁпAD=DBЃЌCA=CBЃЌЁрCDЁЭABЃЌЁрЁЯADC=90ЁуЃЌгЩЂйПЩжЊAЁЂDЁЂMЁЂCЫФЕуЙВдВЃЌЁрЕБІСДг90ЁуБфЛЏЕН180ЁуЪБЃЌЕуMдквдACЮЊжБОЖЕФЁбOЩЯЃЌдЫЖЏТЗОЖЪЧЛЁCDЃЌЁпOA=OCЃЌCD=DAЃЌЁрDOЁЭACЃЌЁрЁЯDOC=90ЁуЃЌЁр![]() ЕФГЄ=
ЕФГЄ=![]() =
=![]() ЃЌЁрЕБІСДг90ЁуБфЛЏЕН180ЁуЪБЃЌЕуMдЫЖЏЕФТЗОЖГЄЮЊ
ЃЌЁрЕБІСДг90ЁуБфЛЏЕН180ЁуЪБЃЌЕуMдЫЖЏЕФТЗОЖГЄЮЊ![]() ЃЎ
ЃЎ


 БИеНжаПМКЎМйЯЕСаД№АИ
БИеНжаПМКЎМйЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаЫФИіНсТле§ШЗЕФЪЧЃЈ ЃЉ
A. ШЮКЮгаРэЪ§ЖМгаЕЙЪ§ B. ЗћКХЯрЗДЕФЪ§ЛЅЮЊЯрЗДЪ§
C. ОјЖджЕЖМЪЧе§Ъ§ D. ећЪ§КЭЗжЪ§ЭГГЦгаРэЪ§
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩЬГЁНЋФГжжЩЬЦЗАДдМлЕФ8елГіЪлЃЌШдПЩЛёРћ20дЊЃЎвбжЊетжжЩЬЦЗЕФНјМлЮЊ140дЊЃЌФЧУДетжжЩЬЦЗЕФдМлЪЧЃЈЁЁЁЁЃЉ
A. 160дЊ B. 180дЊ C. 200дЊ D. 220дЊ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПжБНЧШ§НЧаЮЕФаББпЮЊ10cmЃЌСНжБНЧБпжЎБШЮЊ3ЃК4ЃЌФЧУДетИіжБНЧШ§НЧаЮЕФжмГЄЮЊ______ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЪ§жсЩЯгаЗжБ№БэЪОЁЊ7гы2ЕФСНЕуAЁЂBЃЌШєНЋЪ§жсбиЕуBЖделЃЌЪЙЕуAгыЪ§жсЩЯЕФСэвЛЕуCжиКЯЃЌдђЕуCБэЪОЕФЪ§ЮЊ________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛДЮКЏЪ§y=Љx+2ЭМЯѓОЙ§ЃЈ ЃЉ
A.вЛЁЂЖўЁЂШ§ЯѓЯо
B.вЛЁЂЖўЁЂЫФЯѓЯо
C.вЛЁЂШ§ЁЂЫФЯѓЯо
D.ЖўЁЂШ§ЁЂЫФЯѓЯо
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
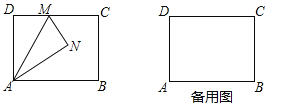
ЁОЬтФПЁПШчЭМЃЌОиаЮABCDжаЃЌAB=4ЃЌAD=3ЃЌMЪЧБпCDЩЯвЛЕуЃЌНЋЁїADMбижБЯпAMЖделЃЌЕУЕНЁїANMЃЎ
ЃЈ1ЃЉЕБANЦНЗжЁЯMABЪБЃЌЧѓDMЕФГЄЃЛ
ЃЈ2ЃЉСЌНгBNЃЌЕБDM=1ЪБЃЌЧѓЁїABNЕФУцЛ§ЃЛ
ЃЈ3ЃЉЕБЩфЯпBNНЛЯпЖЮCDгкЕуFЪБЃЌЧѓDFЕФзюДѓжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєДњЪ§ЪН2x2+3xЉ1ЕФжЕЮЊ1ЃЌдђДњЪ§ЪН4x2+6xЉ1ЕФжЕЮЊЃЈЁЁЁЁЃЉ
A. Љ3B. Љ1C. 1D. 3
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛзщбЇЩњЕФЩэИпЪЧЃЈЕЅЮЛЃКУзЃЉ1.60ЁЂ1.65ЁЂ1.59ЁЂ1.70ЁЂ1.72ЁЂ1.70ЁЂ1.75ЁЂ1.60ЁЂ1.70ЁЂ1.68ЃЌдђетзщбЇЩњЩэИпЪ§ОнЕФМЋВюЪЧ( ).
A.2
B.0.16
C.0.14
D.0
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com