
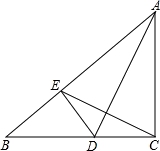
.如图,△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB于E.
求证:直线AD是线段CE的垂直平分线.

【考点】角平分线的性质;全等三角形的判定与性质;线段垂直平分线的性质;直角三角形的性质.
【专题】证明题.
【分析】由于DE⊥AB,易得∠AED=90°=∠ACB,而AD平分∠BAC,易知∠DAE=∠DAC,又因为AD=AD,利用AAS可证△AED≌△ACD,那么AE=AC,而AD平分∠BAC,利用等腰三角形三线合一定理可知AD⊥CE,即得证.
【解答】证明:∵DE⊥AB,
∴∠AED=90°=∠ACB,
又∵AD平分∠BAC,
∴∠DAE=∠DAC,
∵AD=AD,
∴△AED≌△ACD,
∴AE=AC,
∵AD平分∠BAC,
∴AD⊥CE,
即直线AD是线段CE的垂直平分线.
【点评】本题考查了线段垂直平分的定义、全等三角形的判定和性质、等腰三角形三线合一定理,解题的关键是证明AE=AC.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
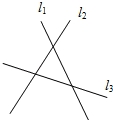
直线 l1、l2、l3 表示三条两两相互交叉的公路,现在拟建一个货物中转站,要求它到三条公路的距离都相等,则可供选择的地址有__________处.
查看答案和解析>>
科目:初中数学 来源: 题型:
 △ABC≌△AEF,有以下结论:
△ABC≌△AEF,有以下结论:
①AC=AE;②∠FAB=∠EAB;③EF=BC; ④∠EAB=∠FAC,
其中正确的个数是( )

A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
已知:如图,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E三点在同一直线上,连接BD.
求证:(1)△BAD≌△CAE;(2)试猜想BD、CE有何特殊位置关系,并证明.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com