
 如图,在Rt△ABC中,∠BAC=90°,AB=AC=2,点D为BC上一点且与B、C不重合.∠ADE=45°,交AC于E.
如图,在Rt△ABC中,∠BAC=90°,AB=AC=2,点D为BC上一点且与B、C不重合.∠ADE=45°,交AC于E.分析 (1)根据等腰直角三角形的性质及三角形内角与外角的关系,易证△ABD∽△DCE;
(2)由△ABD∽△DCE,对应边成比例及等腰直角三角形的性质可求出y与x的函数关系式;
(3)由题意得到∠DAE<∠BAC<90°,由∠ADE=45°,于是得到当△ADE是直角三角形时,只有∠AED=90°,推出△AED是等腰直角三角形,于是得到结论.
解答 解:(1)△ABD与△DCE相似,
∵∠BAC=90°,AB=AC,
∴∠B=∠C=∠ADE=45°,
∵∠ADC=∠B+∠BAD=∠ADE+∠CDE,
∴∠BAD=∠CDE,
∴△ABD∽△DCE;
(2)由(1)得△ABD∽△DCE
∴$\frac{BD}{CE}=\frac{AB}{CD}$
∵∠BAC=90°,AB=AC=2,
∴BC=2$\sqrt{2}$,DC=2$\sqrt{2}$-x,EC=2-y
∴$\frac{x}{2-y}=\frac{2}{2\sqrt{2}-x}$,
∴y=$\frac{1}{2}$x2-$\sqrt{2}$x+2;
(3)∵∠DAE<∠BAC,
∴∠DAE<90°,
∵∠ADE=45°,
∴当△ADE是直角三角形时,
只有∠AED=90°,
∴△AED是等腰直角三角形,
∴AE=DE,∠DAE=45°,
∴∠ADC=90°,
∴AC=CD,
∴AE=$\frac{1}{2}$AC=1.
点评 本题考查了相似三角形的判定和性质,等腰直角三角形的性质,求二次函数的解析式,熟练掌握相似三角形的判定和性质定理是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
 如图,将Rt△ABC绕直角顶点顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=22°,则∠B的度数是( )
如图,将Rt△ABC绕直角顶点顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=22°,则∠B的度数是( )| A. | 67° | B. | 62° | C. | 82° | D. | 72° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
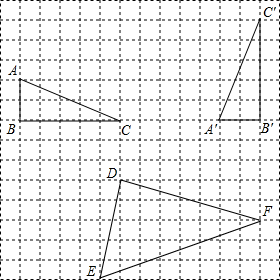 在如图所示的方格图中,每个小正方形的顶点成为“格点”,且每个小正方形的边长均为1个长度单位,以格点为顶点的图形叫做“格点图形”,根据图形解决下列问题:
在如图所示的方格图中,每个小正方形的顶点成为“格点”,且每个小正方形的边长均为1个长度单位,以格点为顶点的图形叫做“格点图形”,根据图形解决下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
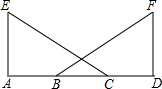 如图,已知点A,B,C,D在同一条直线上,EA⊥AB,FD⊥AD,AB=CD,若用“HL”证明Rt△AEC≌△Rt△DFB,需添加什么条件?并写出你的证明过程.
如图,已知点A,B,C,D在同一条直线上,EA⊥AB,FD⊥AD,AB=CD,若用“HL”证明Rt△AEC≌△Rt△DFB,需添加什么条件?并写出你的证明过程.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
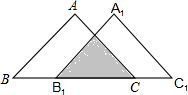 如图,将等腰直角△ABC沿BC方向平移得到△A1B1C1.若B1C=3$\sqrt{2}$.△ABC与△A1B1C1重叠部分面积为$\frac{9}{2}$.
如图,将等腰直角△ABC沿BC方向平移得到△A1B1C1.若B1C=3$\sqrt{2}$.△ABC与△A1B1C1重叠部分面积为$\frac{9}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com