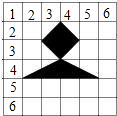
小明在玩一种叫“掷飞镖的游戏.如果小明将镖随意投中如图所示的正方形木板.那么镖落在阴影部分的概率是$\frac{1}{9}$．题目和参考答案——青夏教育精英家教网—

14．

小明在玩一种叫“掷飞镖”的游戏，如果小明将镖随意投中如图所示的正方形木板，那么镖落在阴影部分的概率是$\frac{1}{9}$．

分析首先借助网格求出阴影部分面积，进而利用概率公式求出答案．

解答解：如图所示：
阴影部分的面积为：$\sqrt{2}$×$\sqrt{2}$+$\frac{1}{2}$×1×4=4，
故镖落在阴影部分的概率是：$\frac{4}{36}$=$\frac{1}{9}$．
故答案为：$\frac{1}{9}$．

点评此题主要考查了几何概率，根据题意得出阴影部分面积是解题关键．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：填空题

4．若一个三角形的三条边满足：一边等于其他两边的平均数，我们称这个三角形为“平均数三角形”．
（1）下列各组数分别是三角形的三条边长：
①5，7，5； ②3，3，3； ③6，8，4； ④1，$\sqrt{3}$，2．
其中能构成“平均数三角形”的是②③；（填写序号）
（2）已知△ABC的三条边长分别为a，b，c，且a＜b＜c．若△ABC既是“平均数三角形”，又是直角三角形，则$\frac{a}{b}$的值为$\frac{3}{4}$．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

5．

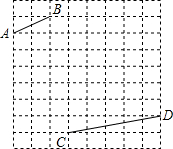如图的方格纸中，每个小正方形的边长均为1，有线段AB和线段CD，线段的端点均在小正方形的顶点上．
（1）在方格纸中画出分别以线段AB，CD为一边的两个三角形，使这两个三角形关于某条直线成轴对称，且两个三角形的顶点均在小正方形的顶点上．
（2）请直接写出一个三角形的面积．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

2．不等式$\left\{\begin{array}{l}{x＞2}\\{x＜a}\end{array}\right.$无解，则a的取值范围是（　　）

A．

a＜2

B．

a＞2

C．

a≤2

D．

a≥2

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

9．阅读下列材料：
解答“已知x-y=2，且x＞1，y＜0，试确定x+y的取值范围”有如下解法：
解∵x-y=2，∴x=y+2．
又∵x＞1，∴y+2＞1．
∴y＞-1．
又∵y＜0，∴-1＜y＜0．　…①
同理得：1＜x＜2．　　…②
由①+②得-1+1＜y+x＜0+2
∴x+y的取值范围是0＜x+y＜2
请按照上述方法，完成下列问题：
（1）已知x-y=4，且x＞3，y＜1，则x+y的取值范围是2＜x+y＜6．
（2）已知y＞1，x＜-1，若x-y=m成立，求x+y的取值范围（结果用含m的式子表示）．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

19．

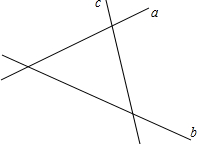如图，有三条公路a，b，c，为了方便司机休息，路政部门确定修建一个休息站P，使它到三条公路的距离相等．（请用尺规作图，保留作图痕迹，不写作法．）